Introducción:
Hola nuevamente hoy vamos a ver el tema del teorema de Pitágoras, específicamente veremos una de sus demostraciones (ya que de hacer más demostraciones tendría que hacer más dibujos…🙄), la verdad fue complicado ya que no conseguía explicarlo forma adecuada.
Escribí muchos borradores del tema en papel y cada que lo pasaba a limpio el ojo observador de Kj encontraba un error y aunque yo replicaba en mi defensa solo me embarraba más, ya que ni de forma escrita ni oral podía darme a entender.

¿Qué es el teorema de Pitágoras?
Es un fórmula que nos ayuda a encontrar los lados o catetos de un triángulo rectángulo, nótese bien que el teorema de Pitágoras funciona solo para el triángulo rectángulo o triángulos donde uno de sus ángulos es de 90º.
Teorema de Pitágoras
La hipotenusa elevado al cuadrado es igual a la suma de los dos catetos elevados también al cuadrado.
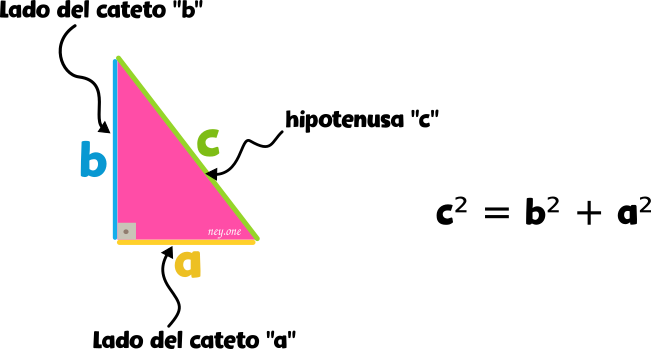
Demostración del teorema de Pitágoras
Paso 1.
Sabemos que la formula del teorema de Pitágoras es c²=b²+a² y también sabemos que cualquier número X elevado al cuadrado se puede interpretar como área de un cuadrado de lado X (ver fórmula del cuadrado abajo).
Entonces c, b y a que son los lados del triangulo rectángulo, cuando los elevados al cuadrado se podrían interpretar como el áreas de un cuadrado:
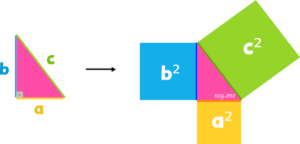
Antes de continuar vamos a detenernos un momento para recordar la fórmula del área de un cuadrado y aplicarla a cada cuadrado formado por los lados del triangulo rectángulo.
Área de un cuadrado

Área de los cuadrados formados a partir de cada lado

Paso 2.
Ahora vamos a continuar, tomamos los cuadrados de los lados a y b, y los colocamos de la siguiente forma.

Paso 3.
Formamos un cuadrado nuevo a partir de la posición y los lados de estos cuadrados, este nuevo cuadrado lo llamaremos n .

A primera vista podemos notar que el cuadrado n (cuadrado nuevo) esta formado por 2 cuadrados y 2 rectángulos y a estos rectángulos los dividimos de tal forma que quedan 2 triángulos rectángulos en cada rectángulo.

Paso 4.
Lo siguiente es hallar el área de nuestro cuadrado n (cuadrado nuevo), para ellos vamos a identificar o nombrar sus lados.
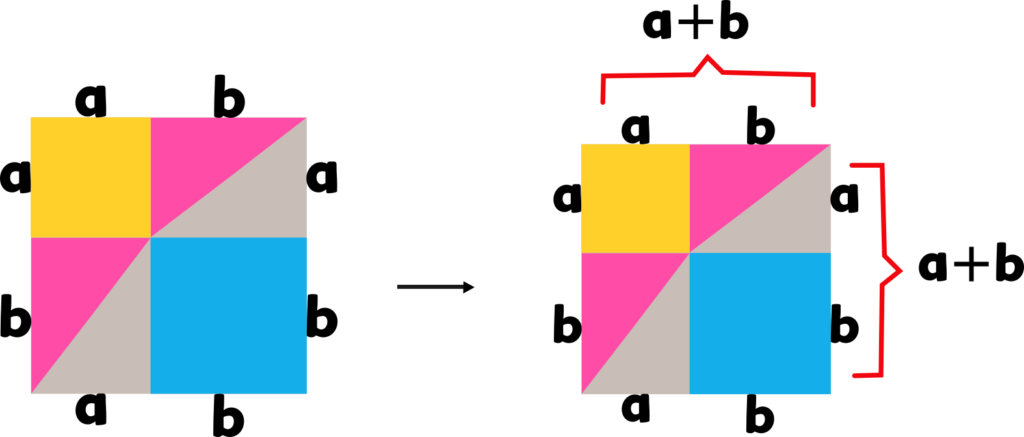
➡️ Fórmula 1
Otra forma de hallar o encontrar el área del cuadrado n (cuadrado nuevo) es sumando el área de las figuras que lo conforman; pero antes de sumar el área de las figuras que lo conforman vamos a recordar la fórmula del área de un triángulo rectángulo.

Ahora sí, sumamos todas las áreas de las figuras internas

Tenemos 4 triángulos rectángulos entonces sumamos el área de estos 4
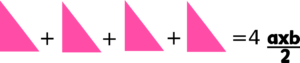
Por lo tanto la suma del área de las figuras internas que forma el cuadrado n es:
Simplificamos
➡️ Fórmula 2
Paso 5.
Igualamos las formulas 1 y 2
➡️ Fórmula 1
➡️Fórmula 2
Igualando
➡️ Fórmula 3
Paso 6.
Para continuar con la demostración tomamos los 4 triángulos rectángulos y el cuadrado n (cuadrado nuevo) y los colocamos de la siguiente forma.

Paso 7.
Y otra vez tenemos que encontrar el área del cuadrado n y también el área de las figuras que lo componen. Para ello vamos a ayudarnos identificando los lados.
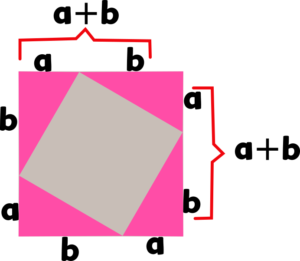
➡️ Fórmula 4
Pero antes de continuar notemos que en un triangulo rectángulo que tiene base a y altura b tendrá también el lado de la hipotenusa c como en el triangulo rectángulo de donde partió la demostración.

Toca encontrar el área de las figuras internas

Entonces la suma del las figuras internas que forman el cuadrado n es:
➡️ Fórmula 5
Paso 8.
Igualamos las formulas 4 y 5
➡️ Fórmula 4
➡️ Fórmula 5
Igualando
Simplificando
➡️ Fórmula 6
Paso 9.
Finalmente igualamos las formulas 3 y 6
➡️ Fórmula 3
➡️ Fórmula 6
Igualando
Simplificamos 2(bxa)
Conclusión:
Y con eso hemos logrado llegar a la fórmula de Pitágoras.
Algo importante que puedo añadir al final de esto es a no confundir la aplicación de una fórmula con su demostración: Mientras que en una aplicación la se usa la fórmula para resolver un problema, en la demostración utilizamos conocimientos previos y lógica para llegar a construir dicha fórmula.


