Problema:
Un cilindro hueco de aluminio de 20.0cm de profundidad tiene una capacidad interna de 2.000 Litros a 20.0°C. Se llena por completo con trementina y luego se calienta a fuego lento a 80.0°C. Calcular ¿Cuánta trementina se desborda?. Considere que el coeficiente térmico lineal del aluminio es 24X10-6 y el coeficiente térmico volumétrico de la trementina es 9.0X10-4, ademas 1 litro = 0.001m3 .
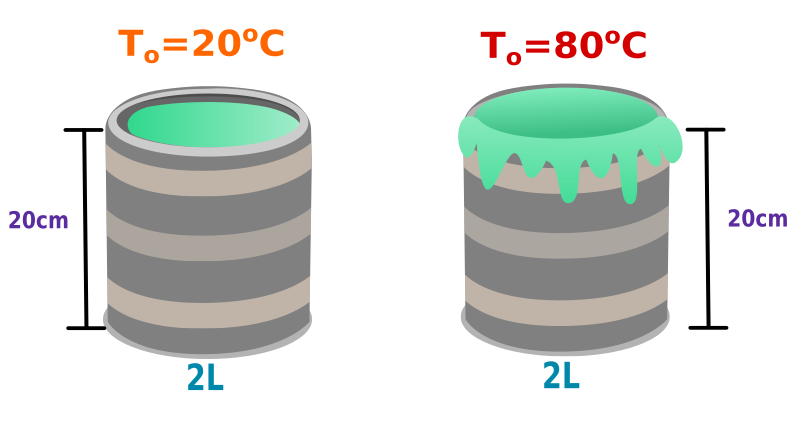
Datos:
Donde:
= Coeficiente térmico lineal del aluminio.
= Temperatura inicial.
= Temperatura final.
= Coeficiente térmico volumétrico de la trementina.
= Incremento de la temperatura.
=Incremento del volumen.
= Coeficiente de expansión volumétrica.
= Volumen inicial.
Formulas:
(1)
(2)
(3)
Cálculos anexos:
Antes de nada convertiremos los 2 litros de la capacidad del cilindro a , debido a que los 2 litros es el volumen inicial del aluminio y de la trementina.
Si entonces
.
Solución:
Para hallar el desborde que se produce con el incremento de la temperatura, debemos restar el incremento de volumen del aluminio con el de la trementina. Pero antes es imprescindible conocer el valor del incremento de la temperatura y el coeficiente de expansión volumétrica del aluminio.
Primero:
Vamos a hallar el valor del incremento de la temperatura, haciendo la diferencia entre Tf y To:
Segundo:
Hallamos el coeficiente de expansión volumétrica del aluminio, multiplicando por 3 su valor:
Tercero:
Encontramos el incremento de volumen del aluminio con la formula (3):
Cuarto:
Encontramos el incremento de volumen de la trementina con la formula (3):
Nota: Recuerde que en el problema ya nos da «el coeficiente térmico volumétrico de la trementina«, no necesitamos multiplicarlo por 3 como en el caso del aluminio.
Quinto:
Teniendo los 2 incrementos de volumen, hallamos el volumen derramado de la trementina :
Redondeando:
Expresándolo en notación científica:
Si encuentras algún error por favor déjalo en los comentarios, para que pueda rectificar el ejercicio.



Cuando pasaste todo a cientifica sobre el final olvidaste copiar un digito.
Oh, cierto al pasar el resultado a notación científica olvide ponerle el número 9 después del punto. ¡Gracias por la corrección!…😃
Gracias
¡Gracias por el gracias! xD
En el valor desbordado cuando se resta 0.108 m^3 – 0.008694 m^3
Ese valor sale 0.09936 m^3, es una observación.
En realidad el error esta más arriba, en los puntos en los que en encontramos el volumen de la trementina y el volumen del aluminio olvide colocar más ceros por eso el resultado es correcto 0.0000994m3.
Bueno gracias a tu comentario ya lo corregí :).
hola
te saltaste el paso de coeficiente de expansión volumétrica de trementina.
No, en el enunciado del ejercicio ya le dan este valor.
¿Cuál valor?
falto Btre=3(9.0×10-4) =2.7?, o se tiene que pasar directo?.
Se pasa directo porque ese 9.0×10-4 ya esta en coeficiente de expension volumetrica.
Parece que me salte un paso y eso modifico todo el resultado, sorry lo voy a corregir. :/
Ok, ya se que paso, pasa que te confundiste, a ver, en el aluminio tenemos el coeficiente térmico lineal del aluminio por eso lo convertimos a coeficiente térmico volumétrio; pero el dato de la trementina ya es un coeficiente térmico volumétrio.
Por eso ya no es necesario hacer ese paso en la trementina.
me puedes explicar el paso donde calculas la expansion volumetrica del aluminio si no es macizo?
Aquí te dejo una imgen que espero te ayude.
Bibliografia del ejercicio porfa
No hay, el docente solo nos dio el ejercicio.
Dice 2000L, no 2