Ejercicio de Movimiento armónico simple| Energía 016 | Ney

Publicidad

Problema:

Un objeto se mueve en movimiento armónico simple con periodo de 0.8s y aceleración máxima de 6.5m/s². Calcule su rapidez máxima.

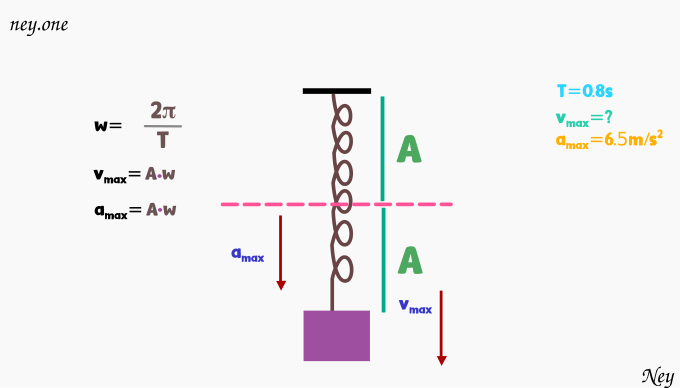
Datos:

$T=0.8s$

$a_{max}=6.5m/s^2$

$V_{max}=?$

Fórmulas:

1) $\boldsymbol{ \omega = \frac{2\pi}{T} }$

2) $\boldsymbol{ a_{max}= A \times \omega^2 }$

3) $\boldsymbol{ V_{max}= A \times \omega }$

Donde:

$K$ = Constante [N/m].

$v$ = Velocidad del objeto [m/s].

$A$ = Amplitud [m].

$a_{max}$ = Aceleración máxima [m/s²].

$\omega$ = Frecuencia angular [rad/s].

$T$ = Periodo [s].

$V_{max}=?$ Velocidad máxima [m/s].

Solución:

Publicidad

Este ejercicio es sencillo y fácil como veremos a continuación y para resolverlo solo tenemos que aplicar las 3 fórmulas de más arriba.

Primero:

Para resolver el problema primero encontramos el valor de la frecuencia angular (w)

$\boldsymbol{ \omega = \frac{2\pi}{T} }$

$\boldsymbol{ \omega = \frac{2\pi}{0.8s} }$

$\boldsymbol{ \omega = 7.854 \frac{rad}{s} }$

Segundo:

Como ya tenemos la frecuencia angular (w), ahora toca encontrar la amplitud (A) para ello la despejamos de la fórmula de la aceleración máxima.

$\boldsymbol{ a_{max}= A \times \omega^2 }$

$\Large{ \boldsymbol{ \frac{a_{max}}{\omega^2} = A } }$

$\Large{ \boldsymbol{ A= \frac{a_{max}}{\omega^2} } }$

$\Large{ \boldsymbol{ A= \frac{6.5 \frac{m}{s^2} }{7.854^2\frac{rad}{s^2} } } }$

$\Large{ \boldsymbol{ A= 0.10537m } }$

Tercero:

Como ya tenemos la amplitud (A) y la frecuencia angular (w), ahora podemos encontrar la rapidez máxima.

$\boldsymbol{ V_{max}= A \times \omega }$

$\boldsymbol{ V_{max}= 0.10537m \times 7.85\frac{rad}{s} }$

$\boldsymbol{ V_{max}= 0.827\frac{m}{s} }$

Con esto resolvimos finalmente el problema y hallamos la $V_{max}$

Publicidad

Relacionado

Categorías: FísicaMovimiento armónico simple

Etiquetas: aceleración máxima de 6.5m/s²Ejercicio de Movimiento armónico simple| Energía 016m.a.s.Un objeto con periodo 0.08s

Subscribe

0 Comments

Inline Feedbacks

View all comments