Física II – Ejercicio de Gravitación 06

Problema:

Cuatro masas idénticas de 800kg cada una se colocan en las esquinas de un cuadrado que mide 10.0cm por lado. ¿Qué fuerza gravitacional neta actúa sobre una de las masas debido a las otras 3?.

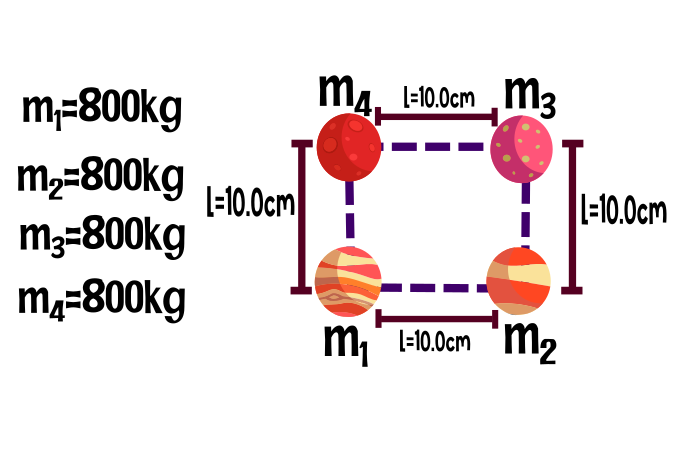
Datos:

$m_1= 800kg$

$m_2=800kg$

$m_3=800kg$

$m_4=800kg$

$L=10.0cm$

$G=6.67\times 10^{-11}\frac{N\times m^2}{kg^2}$

$F_t=?$

Donde:

$m=$ Masa.

$L=$ Longitud.

$F_t=$ Fuerza neta o total.

$G=$ Constante de gravitación universal.

$r=$ Radio.

$g=$ Gravedad.

Formulas:

(1) ${\Large F=G\times \frac{M \times m}{r^2}}$

(2) $c= \sqrt[2]{a^2 +b^2}$

(3) $F=m\times g$

Solución:

En palabras sencillas la pregunta del problema es ¿Cuál es la fuerza de atracción que ejercen las tres masas sobre la primera?. Entonces para resolverlo debemos hallar la gravedad de cada una de las masa que actúan sobre la $m_1$ , para ello usaremos la formula (1) y (2) y obtendremos la gravedad.

Primero:

Reemplazamos la formula 3 en 1 .

(1) ${\Large F=G\times \frac{M \times m}{r^2}}$

(3) $F=m\times g$

${\Large m\times g=G\times \frac{M \times m}{r^2}}$

Dividimos ambos miembros por (1/m) de esta forma simplificamos la masa m y la gravedad queda despejada.

${\Large m\times g=G\times \frac{M \times m}{r^2}}$ $\times (\frac{1}{m})$

${\Large g=G\times \frac{M}{r^2}}$ —>(4)

Segundo:

Hallamos el radio que hay entre la masa uno y las otras tres masas.

Radio entre $m_1$ y $m_2$

$10.0cm\times\frac{0.01m}{1cm}= 0.1m$

$r_{1,2}=0.1m$

Radio entre $m_1$ y $m_3$

Usando el teorema de Pitágoras hallamos el radio entre las masas y que como se ve en la figura forman un triangulo rectángulo.

${\Large r_{1,3}= \sqrt[2]{0.1^2 +0.1^2}= 0.141421358m}$

Radio entre $m_1$ y $m_4$

$r_{1,4}= 0.1m$

Tercero:

Usando la formula 4 hallamos la gravedad de las tres masas ya que ahora tenemos también sus respectivos radios.

Gravedad de la masa 2.

${\Large g=G\times \frac{M}{r^2}}$

${\Large g_2=G\times \frac{M_2}{r_{1,2}^2}}$

${\Large g_2=6.67\times10^{-11}\frac{N\times m^2}{kg^2}\times \frac{800kg}{0.1m^2}}$

$g_2= 0.000005336\frac{N}{kg}$

Gravedad de la masa 3.

${\Large g=G\times \frac{M}{r^2}}$

${\Large g_3=G\times \frac{M_3}{r_{1,3}^2}}$

${\Large g_3=6.67\times10^{-11}\frac{N\times m^2}{kg^2}\times \frac{800kg}{0.141421358m^2}}$

$g_3=0.0000002668\frac{N}{kg}$

Debido a que la gravedad de la masa 3 forma un angulo de 45º, hallaremos su valor en «x» y «Y»

$g_{3x}=0.0000002668\frac{N}{kg}\times cos 45=0.000000188\frac{N}{kg}$

$g_{3y}=0.0000002668\frac{N}{kg}\times sen 45=0.000000188\frac{N}{kg}$

$g_{3t}=0.000000372\frac{N}{kg}$

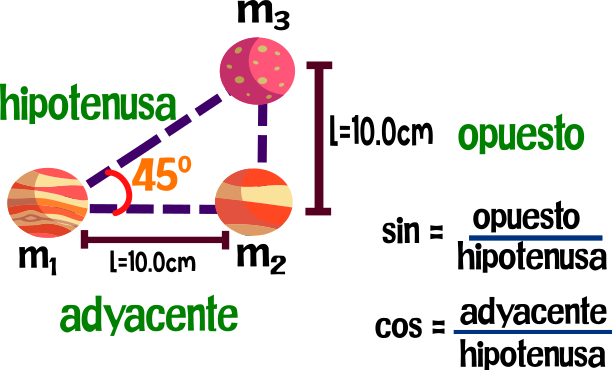
expresado en notación científica.

${\Large g_{3t}=3.72\times 10^{-7}\frac{N}{kg}}$

Gravedad de la masa 4.

${\Large g=G\times \frac{M}{r^2}}$

${\Large g_4=G\times \frac{M_4}{r_{1,4}^2}}$

${\Large g_4=6.67\times10^{-11}\frac{N\times m^2}{kg^2}\times \frac{800kg}{0.1m^2}}$

${\Large g_4= 0.000005336\frac{N}{kg}}$

Sumamos las gravedades.

$g_t= g_2+g_3+g_4$

$g_t= 0.000005336\frac{N}{kg}+0.000000372\frac{N}{kg}+0.000005336\frac{N}{kg}=0.000011044\frac{N}{kg}$

Cuarto:

Finalmente para hallar la Fuerza de atracón entre la masa y las otras tres usamos la formula 3.

$F=m\times g$

$F_t=m_1\times g_{2,3,4}$

$F_t=800kg\times 0.000011044\frac{N}{kg}= 0.0088352N$

Expresado en notación científica.

$F_t=8.83\times 10^{-3}N$

Conclusión: La fuerza de atracción de las 3 masas ejercidas sobre la primer masa es $8.83\times 10^{-3}N$ .

Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.

Física II – Ejercicio de Gravitación 06

Publicado por Ney en 18 julio, 201918 julio, 2019

Relacionado

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015

Física II – Ejercicio de Gravitación 06

Publicado por Ney en 18 julio, 201918 julio, 2019

Relacionado

Entradas relacionadas

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015