Física II – Ejercicio de Gravitación 05

Introducción:

Para este ejercicio la imagen del problema sera distinto, un poco más kawaii, ya que en mi cabeza todo esto tiene sentido y mola mucho (‘ .‘ ).

Problema:

Expresar en función del radio de la tierra. A que distancia de la misma un objeto que tiene una masa de 1kg pesaría 1N.

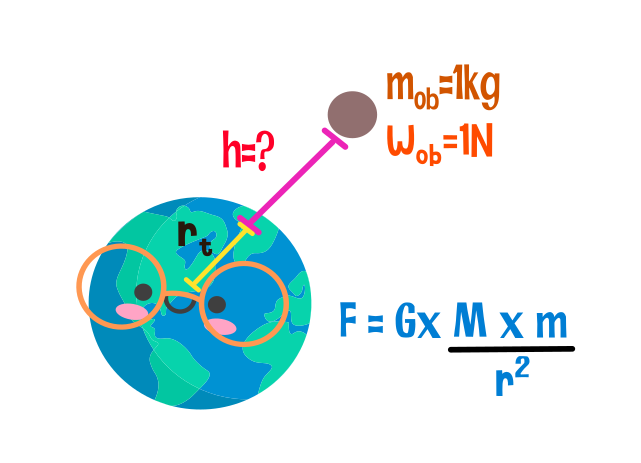
Datos:

$r_t$

$h$

$M_t$

$m_{ob}=1kg$

$W_{ob}=1N$

$G= 6.67\times 10^{-11}\frac{N\times m^2}{kg^2}$

$g = 9.8 \frac{m}{s^2}$

Donde:

$g =$ Gravedad.

$G =$ Constante de gravitación universal.

$W_{ob} =$ Peso del objeto.

$m_{ob}=$ Masa del objeto.

$r_t =$ Radio de la tierra.

$h =$ Altura del objeto.

$M_t =$ Masa de la tierra.

Formulas:

(1) ${\Large F = G\times \frac{m_1\times m_2}{r^2}}$

(2) ${\Large g = G\times \frac{m}{r^2}}$

Solución:

Usaremos la formula (1) y la adaptaremos al problema que vamos a resolver.

Primero:

La masa 1 sera la masa de la tierra, el radio sera la altura a la que se encuentra el objeto y la masa 2 sera la masa del objeto.

${\Large F = G\times \frac{m_1\times m_2}{r^2}}$

${\Large F = G\times \frac{M_t\times m_{ob}}{h^2}}$

Ahora despejamos la altura.

${\Large F \times h^2 = G\times M_t\times m_{ob}}$

${\Large h^2 = G\times \frac{M_t\times m_{ob}}{F}}$ —>(3)

Segundo:

Como ya tenemos la altura despejada, Modificamos un poco la formula (2) para posteriormente reemplazarla en la (3)

${\Large g = G\times \frac{m}{r^2}}$

En esta formula la masa y el radio son de la tierra.

${\Large g = G\times \frac{M_t}{r_t^2}}$

${\Large g \times r_t^2= G \times M_t}$ —>(4)

Si observamos notaremos que en la formula (3) tenemos la masa de la tierra y la constante de gravitación universal y en la formula (4) también y es equivalente al radio de la tierra por la gravedad, entonces reemplazamos la formula (4) en la (3).

${\Large h^2 = G\times \frac{M_t\times m_{ob}}{F}}$ —>(3)

${\Large g \times r_t^2= G \times M_t}$ —>(4)

${\LARGE h^2 = g \times r_t^2\times\frac{m_{ob}}{F}}$

${\LARGE h^2 = g \times r_t^2\times \frac{m_{ob}}{F}}$

Ahora como el orden de los factores no altera el producto, modificamos la posición de las variables, por comodidad.

${\LARGE h^2 = g \times \frac{m_{ob}}{F} \times r_t^2}$

El cuadrado pasa a dividir, desarrollamos y por ultimo reemplazamos valores.

${\Large h = \sqrt[2]{g \times \frac{m_{ob}}{F} \times r_t^2}}$

${\Large h = \sqrt[2]{g \times \frac{m_{ob}}{F}} \times \sqrt[2]{r_t^2}}$

${\Large h = \sqrt[2]{g \times \frac{m_{ob}}{F}} \times r_t}$

El peso es una fuerza y como tal el peso del objeto lo reemplazamos en la fuerza.

${\Large h = \sqrt[2]{9.8\frac{m}{s^2} \times \frac{1kg}{1N}} \times r_t}$

${\Large h =3.130495 r_t}$

Redondeando a dos decimales.

${\Large h =3.13r_t}$

Conclusión: El objeto de 1kg de masa está a una altura de 3.13r_t.

Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.

Física II – Ejercicio de Gravitación 05

Publicado por Ney en 11 julio, 201911 julio, 2019

Relacionado

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015

Física II – Ejercicio de Gravitación 05

Publicado por Ney en 11 julio, 201911 julio, 2019

Relacionado

Entradas relacionadas

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015