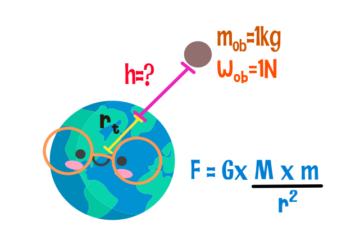
Física II – Ejercicio de Gravitación 03

Problema:

La masa de la luna es 1/81 de la masa de la tierra y su radio es 1/4 del radio de la tierra. Calcular lo que pesaría en la superficie de lunar,si una persona que tiene una masa de 70kg.

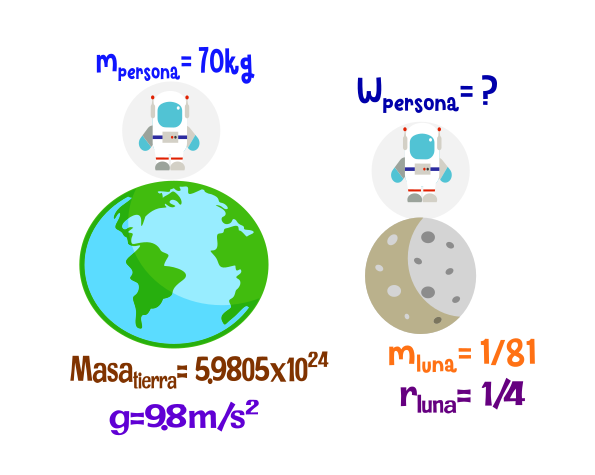
Datos:

$masa_{luna} = 1/81$

$r_{luna} = 1/4$

$W_{persona}=?$

$m_{persona}=70kg$

$G = 6.67\times 10^{-11}N\times \frac{m^2}{kg^2}$

$r_{t}= 6.38\times 10^6m$

$g = 9.8\frac{m}{s^2}$

Donde:

$W =$ Peso [kg*m/s2].
$F =$ Módulo de la fuerza gravitatoria [N].
$m =$ Masas de un cuerpo [kg].
$r =$ Distancia de separación [m].
$G =$ Constante de gravitación universal [N*m²/kg²].
$g =$ Gravedad [m/s²].
$r_t=$ Radio de la tierra.
$m_p=$ Masa de la persona.

Formulas:

(1) $F = G\times \frac{m_1 \times m_2}{r^2}$

(2) $m_t = g\times\frac{r_t^2}{G}$

(3) $g = G\times\frac{m_t}{r_t^2}$

Solución:

Tenemos el radio de la tierra y con ese dato encontraremos la masa de la tierra ya que ese dato no lo tenemos, luego usando la formula (1) encontraremos el peso de la persona de 70kg en la luna.

Nota: Si el valor de una masa es 70kg el peso de esta misma en la tierra es $W = m\times g$ $W = 70kg\times {9.8m}{s^2} = 686N$ .

Primero:

Hallamos la masa de la tierra.

$m_t = g\times\frac{r_t^2}{G}$

$m_t = 9.8\frac{m}{s^2}\times\frac{(6.38\times 10^6m)^2}{6.67\times 10^{-11}N\times \frac{m^2}{kg^2}}$

$m_t = 5.98\times 10^{24}kg$

Segundo:

Hallamos el peso de la persona de 70kg en la luna.

$F = G\times \frac{m_1 \times m_2}{r^2}$

$F = G\times \frac{m_t \times m_p}{r^2}$

Sabiendo que la masa de la luna es 1/81 de la masa de la tierra y el radio de la luna es 1/4 de el radio de la tierra, dividimos el radio de la tierra y su masa por estas cantidades.

$F = G\times \frac{\frac{m_t}{81} \times m_p}{(\frac{r_t}{4})^2}$

Multiplicamos estrenos y medios.

$F = \frac{G\times m_t \times m_p\times 4^2}{81\times r_t^2}$

$F = \frac{4^2}{81} \times \frac{G\times m_t \times m_p}{r_t^2}$

$F = \frac{16}{81} \times \frac{G\times m_t \times m_p}{r_t^2}$

Notemos que la gravedad es igual a la constante de gravitación por la masa de la tierra dividido entre el radio de la tierra al cuadrado, entonces reemplazamos en nuestra formula.

$g = G\times\frac{m_t}{r_t^2}$

$F = \frac{16}{81} \times g \times m_p$

Reemplazamos los datos.

$F = \frac{16}{81} \times \frac{9.8m}{s^2} \times 70kg$

$F = 135.5N$

Tercero:

De no haber reemplazado la gravedad en la formula quedaría.

$F = \frac{16}{81} \times \frac{G\times m_t \times m_p}{r_t^2}$

$F = \frac{16}{81} \times \frac{6.67\times 10^{-11}N\times 5.98\times 10^{24}kg \times 70kg}{(6.38 \times 10^6m)^2}$

$F = 135.9N$

Conclusión:

El peso de una persona de 70kg en la luna es W=135.5N ya que $W=m\times g= F$

Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.

Física II – Ejercicio de Gravitación 03

Publicado por Ney en 8 julio, 20198 julio, 2019

Relacionado

Física

Física II – Ejercicio de Gravitación 06

Física

Física II – Ejercicio de Gravitación 05

Gravitación

Física II – Ejercicio de Gravitación 04

Física II – Ejercicio de Gravitación 03

Publicado por Ney en 8 julio, 20198 julio, 2019

Relacionado

Entradas relacionadas

Física

Física II – Ejercicio de Gravitación 06

Física

Física II – Ejercicio de Gravitación 05

Gravitación

Física II – Ejercicio de Gravitación 04