Problema:
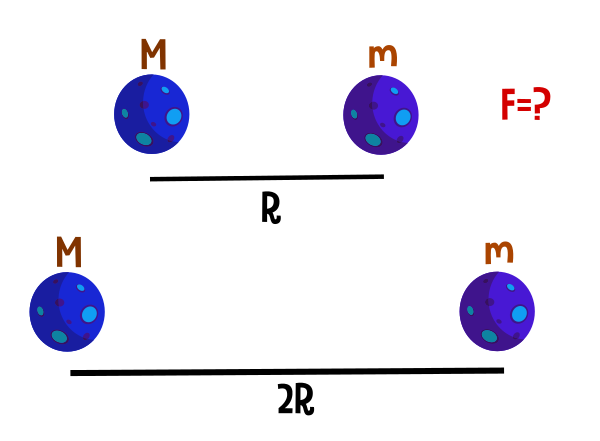
Dos masas, M y m, están separadas a una distancia R . Si se alejan una distancia 2R, ¿Cuál es el módulo de la fuerza gravitatoria que actúa entre ellas?.
Para resolver este problema debemos preguntarnos lo siguiente:
- ¿Qué es la fuerza gravitatoria?.
La fuerza gravitatoria es la atracción entre dos cuerpos, esta atracción depende de sus masas y de la distancia de separación entre ambas. La fuerza de atracción entre los dos cuerpos disminuye al cuadrado de la distancia, es decir que ante un aumento de la distancia entre ellos, el valor de la fuerza de atracción disminuye al cuadrado.
- ¿Qué es el módulo de la fuerza gravitatoria?
Es la cantidad de fuerza de atracción entre 2 cuerpos.
Entonces el módulo de la fuerza gravitatoria se obtiene con la ley de la gravitación universal. Expresándola en formula seria.
Donde:
Módulo de la fuerza gravitatoria [N].
Masas de los cuerpos [kg].
Distancia de separación [m].
Constante de gravitación universal [N·m2/kg2].
Gravedad [m/s2].
Solución:
Inicialmente tenemos 2 masas M y m, que están a una distancia R, estos datos serán reemplazados en la formula de la gravitación universal.
Primero:
Segundo:
Posteriormente las masas se separan una distancia 2R, teniendo porlotanto una nueva fuerza.
Tercero:
Dividimos la fuerza gravitatoria uno y fuerza gravitatoria dos.
Simplificamos la constante de gravitación universal (G), M y m.
Simplificamos el radio.
Conclusión:
La fuerza gravitatoria que actuá entre las dos masas disminuye 4 veces su valor.
Nota: A mayor distancia al cuadrado, menor es la fuerza de gravitación.
Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.