Introducción:
Hace unos días estuve recordando como eran las clases en la secundaria y pensé en escribir un tema sencillo que lleve en aquellos años.
En este tema veremos la suma de vectores de forma gráfica, la verdad tenia pensado escribir otro artículo; pero aun no consigo terminarlo😅… bueno, no más platica y empecemos.
¿Qué es la suma de vectores?
Es la representación de vectores en un solo vector llamado resultante. Entonces la suma de vectores da como resultado un nuevo vector.
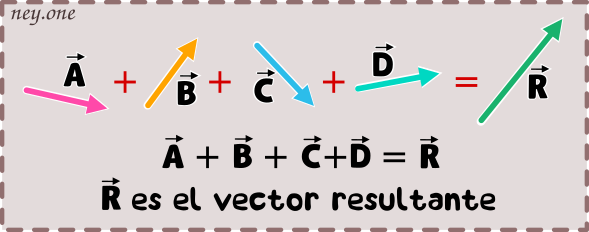
Métodos gráficos para sumar o adicionar vectores
I. Método del paralelogramo
El método del paralelogramo es usado para sumar 2 vectores que sean coplanares y concurrentes.
Para hallar la resultante colocamos o trazamos los 2 vectores en el origen de un plano cartesiano, posteriormente formamos un paralelogramo deslizando los vectores con la ayuda de 2 reglas (una regla recta y una escuadra o 2 escuadras) sin perder el angulo o dimensión.
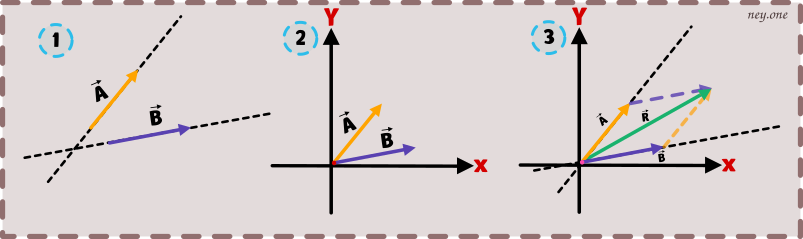
El vector resultante es la diagonal y su punto de aplicación (o punto de inicio) coincide con el punto de aplicación de los anteriores 2 vectores.
II. Método del triángulo
El método del triángulo es válido para sumar 2 vectores que sean nuevamente concurrentes y coplanares.
Se deben colocar o poner los vectores uno a continuación del otro, posteriormente trazamos una linea para cerrar el triángulo y le ponemos el sentido o la flechita (como estamos sumando el sentido de la resultante debe coincidir con el sentido del segundo vector).
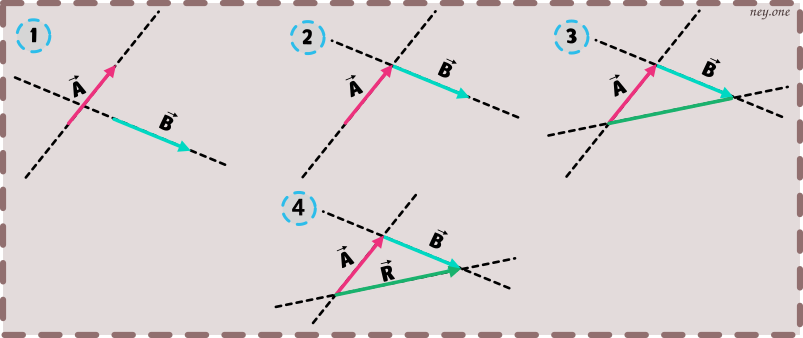
III. Método del polígono
El Método del polígono es usado en caso de 2 o más vectores estos también tienen que ser concurrentes y coplanares.
Para este método vamos a unir los vectores uno a continuación de otro (osea donde termina un vector empieza el siguiente) de esta forma vamos formando el polígono, el punto de aplicación del vector resultante coincide con el punto de aplicación del primer vector.
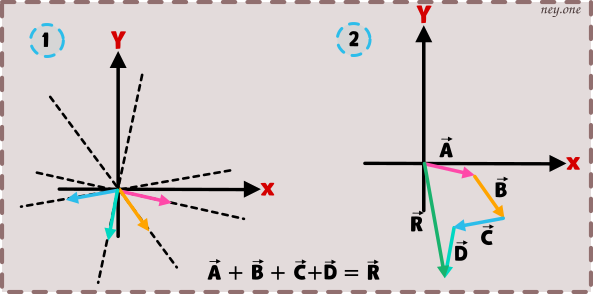
Si el origen del primer vector coincide con el sentido del ultimo vector, el vector resultante es «0» este caso o sistema se llama polígono cerrado.
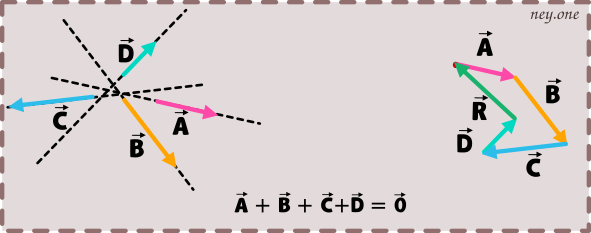
Bueno eso es todo, espero que les sirva de ayuda en algo, ¡hasta luego!😀.


