Física I - Ejercicio de vectores 09 (Sears – Zemansky)

Problema:

Decimos que un objeto está en equilibrio cuando todas las fuerzas sobre él se estabilizan (sumando cero). La figura 1.40 muestra una viga que pesa 124 N y está apoyada en equilibrio por un tirón de 100.0 N y una fuerza F en el piso. la tercer fuerza sobre la viga es el peso de 124N que actúa verticalmente hacia abajo. a) Utilice componentes de vectores para encontrar la magnitud y la dirección de F. b) verifique lo razonable de su respuesta en el inciso a) haciendo una gráfica aproximadamente a escala.

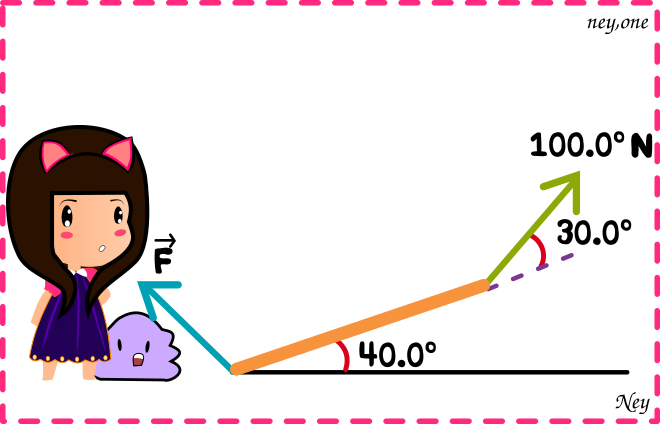
Datos:

$\overrightarrow{F}_{1x}= 100.0 N, \phi=30.0^o$

$\overrightarrow{P}= 124 N$

$\overrightarrow{F}= ?$

$\beta =?$

Donde:

$\overrightarrow{F} =$ $\text{ Vector o Fuerza F.}$

$\overrightarrow{F}_{1x} =$ $\text{ Vector o fuerza F.}$

$\phi=$ $\acute{A}ngulo$ $\text{ del vector}$ $\overrightarrow{F}_{1x}.$

$\beta =$ $\acute{A}ngulo$ $\text{ del vector}$ $\overrightarrow{F}.$

Fórmulas:

$\overrightarrow{F} = \sqrt{\overrightarrow{F_x}^2 + \overrightarrow{Fy}^2}$

$\Large{ \tan \boldsymbol{\theta} = \Bigg(\frac{\overrightarrow{F _y}}{\overrightarrow{F _x}} \Bigg)}$

Solución:

Bien para resolver este problema lo primero que vamos a hacer es graficar el peso y los componentes de las fuerzas.

Nombraremos a la fuerza de 100.0 N como $\overrightarrow{F}_1$ y los componentes de este vector serán « $\overrightarrow{F}_{1x}$ » y « $\overrightarrow{F}_{1y}$ «, mientras que la fuerza del peso de la viga se llamará « $\overrightarrow{P}$ » y la vamos a graficar en el centro de la viga.

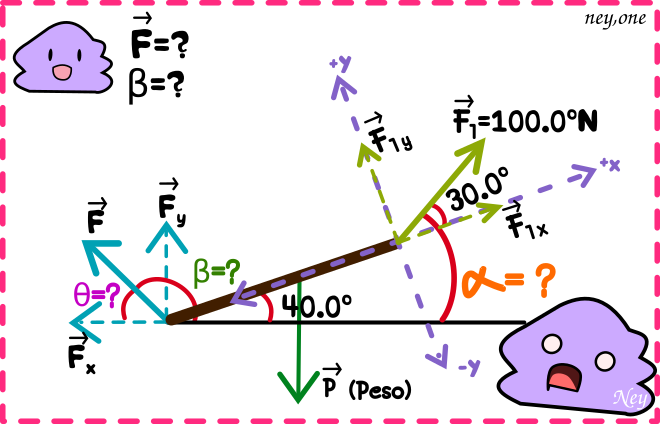
También descompondremos el vector $\overrightarrow{F}$ en sus componentes « $\overrightarrow{F_x}$ » y « $\overrightarrow{F_y}$ «.

Primero:

Antes de hacer la sumatoria de fuerzas vamos a enfocarnos un momento en la fuerza $\overrightarrow{F_1}$ , esta fuerza tiene un ángulo de 30.0º; pero está sobre la viga que tiene un ángulo de 40º entonces la dirección del vector $\overrightarrow{F_1}$ es igual a la suma de el ángulo de 30º mas el ángulo de 40º.

Luego escribimos que del vector $\overrightarrow{F}_1$ al eje x+ hay un ángulo $\alpha$ que es igual a:

$\alpha= 30^o + 40^o =70^o$

Segundo:

Empezamos realizando una sumatoria de fuerzas; pero solo sobre las fuerzas y vectores componentes que estén en el eje x.

$\sum F_x = 0$

$- \overrightarrow{F}_x + \overrightarrow{P} + \overrightarrow{F}_{1x} = 0$

Despejando $\overrightarrow{F_x}$

$- \overrightarrow{F}_x = - \overrightarrow{P} - \overrightarrow{F}_{1x}$

Multiplicando todo por (-1)

$- \overrightarrow{F}_x = - \overrightarrow{P} - \overrightarrow{F}_{1x} * (-1)$

$\overrightarrow{F}_x = \overrightarrow{P} + \overrightarrow{F}_{1x}$

$\overrightarrow{F}_x = 0 + 100 N * \cos 70^o$

$\overrightarrow{F}_x = 34.2 N$

Tercero:

En este punto tenemos que hacer la sumatoria de las fuerzas y/o vectores componentes que estén en el eje y.

$\sum F_y = 0$

$\overrightarrow{F}_y - \overrightarrow{P} + \overrightarrow{F}_{1y} = 0$

Despejamos $\overrightarrow{F}_{y}$

$\overrightarrow{F}_y = \overrightarrow{P} - \overrightarrow{F}_{1y}$

$\overrightarrow{F}_y = 124 N - 100 \sin 70^o$

$\overrightarrow{F}_y = 30.03 N$

Cuarto:

Hasta aquí ya tenemos los vectores componentes y a partir de ello vamos primero a encontrar el vector o fuerza F.

Este vector lo vamos a encontrar con la formula de Pitágoras entonces ponemos:

$\overrightarrow{F} = \sqrt{\overrightarrow{F_x}^2 + \overrightarrow{Fy}^2}$

Reemplazando los valores tenemos:

$\overrightarrow{F} = \sqrt{34.2^2 + 30.03^2}$

$\overrightarrow{F} = 45.5 N$

Redondeando

$\overrightarrow{F} = 46 N$ … $\text{magnitud de la fuerza}$ $\overrightarrow{F}$ .

Quinto:

Ya tenemos la magnitud y vamos a hallar el ángulo de este vector $\overrightarrow{F}$ con la fórmula de la tangente donde:

$\Large{ \tan \boldsymbol{\theta} = \Bigg(\frac{\overrightarrow{F _y}}{\overrightarrow{F _x}} \Bigg)}$

$\Large{ \tan \boldsymbol{\theta} = \Bigg(\frac{30.03}{34.2} \Bigg)}$

$\Large{\boldsymbol{\theta} = \tan^{-1} \Bigg(\frac{30.03}{34.2} \Bigg)}$

$\Large{\boldsymbol{\theta} = 41.28^o}$

No, nos asustemos con este resultado, recordemos que el ángulo de la $\overrightarrow{F}$ debe ir desde el eje x+ hacia el vector. Entonces restamos 41.28º a 180º.

$\Large{\boldsymbol{\beta} = 180^o - \theta}$

$\Large{\boldsymbol{\beta} = 180^o - 41.28^o}$

$\Large{\boldsymbol{\beta} = 138.7^o}$

Redondeando

$\Large{\boldsymbol{\beta} = 139^o}$

Conclusión:

Como pudimos ver la magnitud o módulo del vector $\overrightarrow{F}$ es igual a $46 N$ , mientras que la dirección es $139^o.$

Extra:

También pueden ver el ejercicio resuelto en este vídeo aunque no tiene las correcciones que hice en este post.

Relacionado

3 Comments

Oldest

Newest Most Voted

Inline Feedbacks

View all comments

Rocio

4 years ago

Hola! Gracias pero porque en la sumatoria de fuerzas x se multiplica por -1?

Ney

Author

Reply to Rocio

Multiplicamos x (-1) para que cada miembro de la ecuación se vuelva positivo.

vicente

3 years ago

porque no utilizas el sistema de referencia de forma inclinada, tengo una confusión ese ángulo de 30 esta tomado respecto al plano inclinado y al momento de tu graficarlo le cambias el lugar de donde se esta tomando, estaría muy agradecido que despejaras mis dudas

Física I – Ejercicio de vectores 09 (Sears – Zemansky)

Publicado por Ney en 22 julio, 202022 julio, 2020

Relacionado

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015

Física I – Ejercicio de vectores 09 (Sears – Zemansky)

Publicado por Ney en 22 julio, 202022 julio, 2020

Relacionado

Entradas relacionadas

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015