Demostración de la ley de De Morgan| circuitos lógicos

Definición de la ley de De Morgan

El teorema o ley de «De Morgan» demuestra la equivalencia entre una combinación de compuertas o puerta lógicas.

. Primera ley de De Morgan

La suma lógica negada de las variables lógicas es igual al producto de cada una de dichas variables negadas.

$\overline{A+B} = \overline{A} \bullet \overline{B}$

. Segunda Ley de De Morgan

El producto lógico negado de las variables lógicas es igual a la suma lógica de cada una de las variables negadas.

$\overline{A \bullet B} = \overline{A} + \overline{B}$

Símbolos a usar en la demostración:

Nota: También pondré algunos símbolos que son usados en conjuntos, solo para mostrar que son equivalentes a los símbolos de circuitos lógicos.

$\boldsymbol{ \Rightarrow }$ : Entonces.

$\boldsymbol{ \bullet, \land, \& }$ : Producto lógico (and).

$\boldsymbol{ \lor, + }$ : Suma lógica o disyunción lógica (or).

$\boldsymbol{ -, \neg }$ : Negación.

$\boldsymbol{ \in }$ : Pertenece.

$\boldsymbol{\notin }$ : No pertenece.

Demostración de la 1ra ley de De Morgan

Suponiendo que «x» pertenece a $\overline{A+B}$ , y lo representamos de la siguiente forma:

$\Rightarrow x \in$ $\overline{A+B}$

Entonces:

$\Rightarrow x \notin A+B$

$\Rightarrow x \notin A$ $\&$ $x \notin B$

$\Rightarrow x \in \overline{A}$ $\&$ $x \in \overline{B}$

$\Rightarrow x \in \overline{A} \bullet \overline{B}$

Esta demostración también podemos realizarla partiendo desde $\overline{A} \bullet \overline{B}$ .

Suponiendo que «y» pertenece a $\overline{A} \bullet \overline{B}$ , y lo representamos de la siguiente forma:

$\Rightarrow y \in \overline{A} \bullet \overline{B}$

Entonces:

$\Rightarrow y \notin A$ $\&$ $y \notin B$

$\Rightarrow y \notin A + B$

$\Rightarrow y \in \overline{A + B}$

Este primer teorema también lo podemos representar en una tabla de verdad:

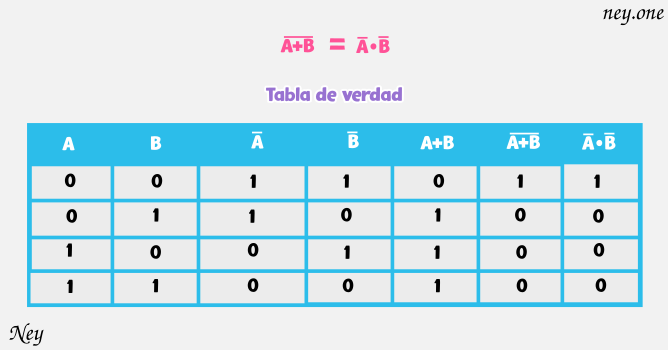
Demostración de la 2ra ley de De Morgan

Suponiendo que «x» pertenece a $\overline{A \bullet B}$ , y lo representamos de la siguiente forma:

$\Rightarrow x \in \overline{A \bullet B}$

Entonces:

$\Rightarrow x \notin A \bullet B$

$\Rightarrow x \notin A$ $\lor$ $x \notin B$

$\Rightarrow x \in \overline{A}$ $\lor$ $x \in \overline{B}$

$\Rightarrow x \in \overline{A} + \overline{B}$

Esta demostración también podemos realizarla partiendo desde $\overline{A} + \overline{B}$

Suponiendo que «y» pertenece a $\overline{A} + \overline{B}$ , y lo representamos de la siguiente forma:

$\Rightarrow y \in \overline{A} + \overline{B}$

$\Rightarrow y \in \overline{A}$ $\lor$ $y \in \overline{B}$

$\Rightarrow y \notin A$ $\lor$ $y \notin B$

$\Rightarrow y \notin A \bullet B$

$\Rightarrow y \in \overline{A \bullet B}$

Este segundo teorema también lo podemos representar en una tabla de verdad:

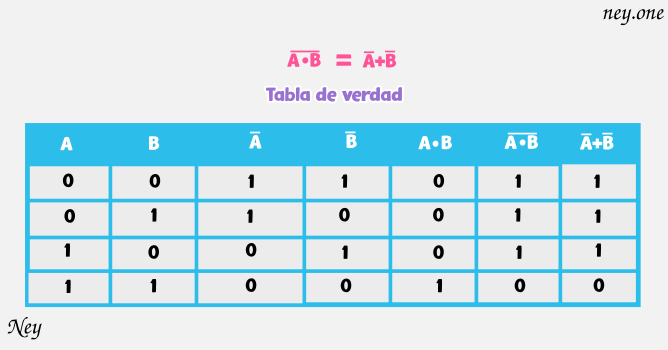
Extra:

También puedes ver estos otros temas:

Si encuentras algún error o algún otro detalle por favor dejalo en los comentarios, para que pueda rectificarlo.🤯

Demostración de la ley de De Morgan| circuitos lógicos

Publicado por Ney en 7 enero, 20217 enero, 2021

Relacionado

Lógica matemática

Algebra I – Leyes de equivalencia lógica

Lógica matemática

Algebra I – Rezumen de operadores lógicos

Lógica matemática

Algebra I – Clasificación de fórmulas proposicionales

Demostración de la ley de De Morgan| circuitos lógicos

Publicado por Ney en 7 enero, 20217 enero, 2021

Relacionado

Entradas relacionadas

Lógica matemática

Algebra I – Leyes de equivalencia lógica

Lógica matemática

Algebra I – Rezumen de operadores lógicos

Lógica matemática

Algebra I – Clasificación de fórmulas proposicionales