Problema:
Un tanque de acero se llena totalmente con 2.80m3 de etanol, el tanque como el etanol están a 32.0°C. Una vez que el sistema se enfría a una temperatura final de 8ºC, ¿Que volumen de etanol se puede adicionar? (Coeficiente de expansión volumétrica del etanol 75X10-5 y Coeficiente de expansión volumétrica del acero 3.6X10-5).
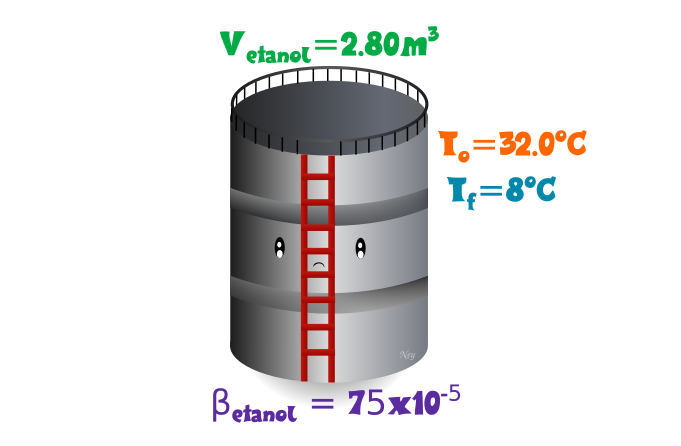
Datos:
Donde:
= Volumen del etanol.
= Temperatura inicial.
= Temperatura final.
= Volumen adicional o cantidad de liquido que le cabe al tanque.
= Coeficiente de expansión volumétrica del etanol.
= Coeficiente de expansión volumétrica del acero.
= Incremento del volumen.
= Incremento de la temperatura.
Formulas:
(1)
(2)
(3)
Solución:
Lo primero por hacer es encontrar el valor del incremento de volumen del acero y del etanol, como ya tenemos el incremento del volumen, hallamos el volumen final del etanol y el acero. Ahora para saber si aun podemos echarle etanol al tanque, vamos a obtener la diferencia entre el volumen final del acero y el volumen final del etanol.
Primero:
Incremento de volumen del acero:
Nota: El volumen del acero es el mismo que del etanol.
Incremento de volumen del etanol:
Segundo:
Volumen final del acero:
Volumen final del etanol:
Tercero:
Diferencia de volumen entre etanol y acero:
Redondeando a dos decimales:
Conclusión: Si ta temperatura final es18°C, el volumen adicional seria 0.048m3.
Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.



Hola, hay un error en su calculo, ya que en la primera ecuacion toma como temperatura final 8 grados, el ejercicio dice 18.
Hola Elkin, muchas gracias por tu comentario ya revise en mis viejos apuntes, y si el dato de 8º es correcto, probablemente mi docente modifico el problema de este ejercicio.
De todas formas el proceso para resolver el problema es el mismo solo cambias 8º por 18º y claro eso modificara el resultado que tengas en la calculadora; pero por lo demás es lo mismo.
si me pide el problema el espacio vacio del tanque sin darme el volumen del acero, pero si el volumen del etanol y la temperatura final e inicial? que hago?
Lo primero es tener la pregunta completa del problema, para tener claro lo que hay que encontrar o resolver.
Al final sacaste que el volumen adicional es de 0.048 pero en la conclusión dices que es 0.028m3, probablemente sea un error de dedo.
Si, así fue me equivoque al poner la conclusión, gracias por corregirme.
Hola, una pregunta, si al final me da 0,084084 m^3 (usando un coeficiente diferente) ¿Es correcto?
Muchas gracias y recoda Hala Madrid y nada más….
porque cuando haces la diferencia de volumen aparece un (-) en el volumen del etanol?