Física II – Ejercicio de Termodinámica 05

Problema:

Las marcas de una regla de aluminio y otra de bronce están perfectamente alineadas a 0°C. ¿Que separación habrá entre las marcas de 20.0cm de las dos reglas a 100°C, si se mantiene una alineación precisa de los extremos izquierdos de las reglas. Coeficiente de expansión lineal del aluminio 2.4X10^-5 C^-1. Coeficiente de expansión lineal del bronce 2.0 X 10^-5 C^-1.

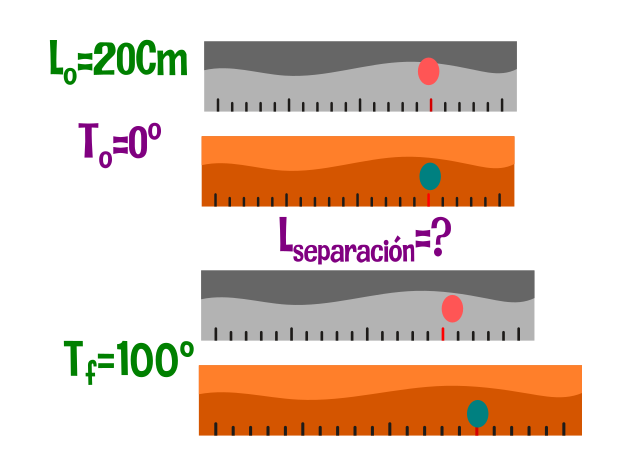
Datos:

Donde:

Formula:

(1)

Cálculos auxiliares:

Antes de comenzar a resolver todo el problema primero vamos a convertir todo lo que este en cm a m.

Una vez teniendo convertido el valor a a la unidad internacional de medidas que es el metro, continuamos con el problema.

Solución:

Para este caso, conviene expresar la pregunta de otra forma puesto que resulta confusa (al menos para mi), La pregunta podría decir: ¿Cuánto se separaran las dos marcas cunado estén a ?.

Para saber cual es la distancia entre ambas marcar, cuando la temperatura llegue a , debemos hallar las longitudes finales, tomando como longitud inicial los 20cm que es donde están las marcas.

Primero:

Hallamos la de la marca del aluminio cuando esta a .

Reemplazamos los valores que tenemos en la formula.

Toca hallar la de la marca del bronce a la misma temperatura.

Segundo:

Reemplazamos los valores que tenemos en la formula nuevamente.

Teniendo las dos longitudes restamos la cantidad mayor con la cantidad menor para hallar la distancia de separación entre ambas.

Tercero:

La distancia es la mayor.

Entonces la distancia de separación es 0.0004m y ahora lo expresamos en cm también:

Si encuentras algún error por favor déjalo en los comentarios, para que pueda rectificar el ejercicio.