Física II – Ejercicio de Termodinámica 03

Problema:

Dos losas de concreto de un puente de 200m de largo se colocan justo en sus extremos, de modo que no se permite espacio para expansión. Si ocurre un aumento de temperatura de 20.0°C, ¿Cuál es la altura a la cual las losas se elevan cuando se pandean?.

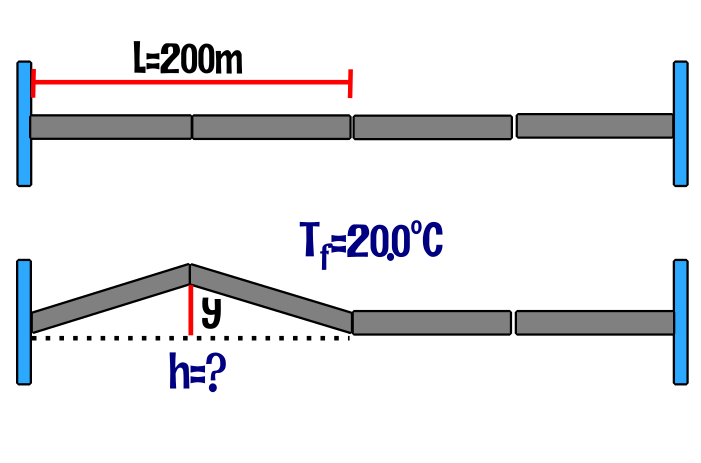
Datos:

$L_o = 200m$

$T_f = T_o + 20^oC$

$h = ?$

$\alpha = 12\times 10^-6^{\circ} C^{-1}$

$L_f = ?$

Donde:

$T_o =$ Temperatura inicial.

$L_f =$ Longitud final.

$L_o =$ Longitud inicial.

$\alpha =$ Coeficiente de expansión lineal.

$\Delta T =$ Incremento de la temperatura.

$a,b =$ Catetos.

$c =$ Hipotenusa.

Formulas:

(1) $L = L_o\times( 1+ \alpha\times \Delta T )$

(2) $b = \sqrt[2]{c^2-a^2}$

(3) $\Delta T = T_f - T_o$

Solución:

De momento lo más sencillo de obtener es $\Delta T$ que luego la usaremos para reemplazarla en la formula de la longitud final; pero primero lo primero.

Hallamos el incremento de la temperatura:

$\Delta T = T_f - T_o$

$T_f = T_o + 20^oC$

Si $T_f$ vale $T_o + 20^oC$ entonces lo reemplazamos en la formula para hallar $\Delta T$ .

Reemplazar:

$\Delta T = T_f - T_o$

$\Delta T = T_o + 20^oC - T_o$

Notamos que $T_o$ y $T_o$ se anulan.

Restamos $T_o$ positiva con $T_o$ negativa y listo :

$\Delta T = 20^oC$

Ahora como tenemos $\Delta T$ , $\alpha$ y $L_o$ lo Reemplazamos en la formula de longitud final.

Reemplazando (1):

$L = L_o\times( 1+ \alpha\times \Delta T )$

$L = 200m\times( 1+ 12\times 10^-6^{\circ} C^{-1}\times 20^oC )$

$L =200.048m$

Cuando las losas se elevan forman un triangulo rectángulo, así que valiéndonos de la formula de Pitágoras hallamos el cateto opuesto (el que esta en vertical a la superficie).

Pero antes dividimos entre 2 la $L_f$ y $L_o$ .

¿Por que? -R. Simple, por que el punte mide 200m y son 2 losas, por ende asumimos que ambas miden la mitad del puente (aun que de ambas solo usamos una losa para hallar la altura).

$L_f =\frac{200.048m}{2}$