Física II – Ejercicio de Termodinámica 010

Introducción:

Revisando mi cuaderno de apuntes de física encontré un ejercicio de termodinámica que no termine de resolver en clase, así que se me ocurrió terminarlo y mostrárselos, así que, aquí se los dejo.

Problema:

Hay un cilindro de acero de 50cm de diámetro, el cilindro esta a 17ºC y un aro de 49.92cm de diámetro debe ser encajado en el. Calcular la temperatura final para ajustar el cilindro.

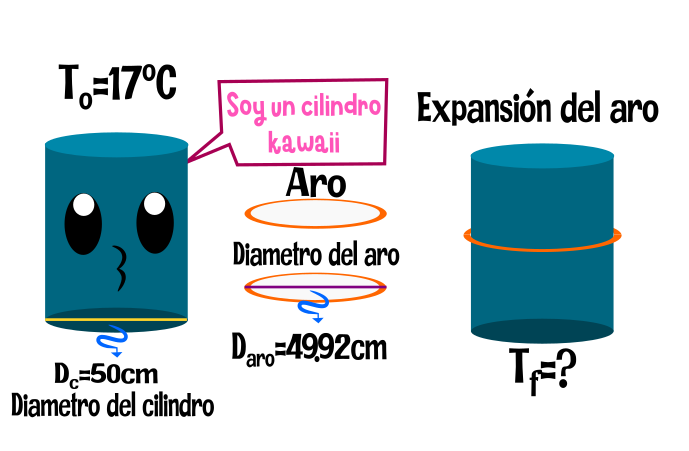
Datos:

$D_c=50cm$

$T_c=17^oC$

$D_{Aro}= 49.92cm$

$T_f=?$

$\alpha=1.2\times 10^{-5} \frac{1}{^oC}$

Formulas:

Fórmula del área de un círculo

(1) $A_{c\acute{i}rculo}=\Pi \times \frac{D^2}{4}$

Fórmula de expansión del área

(2) $\Delta A=A_o + 2\alpha \times A_o(T_f - T_o)$

Donde:

$D_c=$ Diámetro del cilindro [m].

$D_{aro}=$ Diámetro del aro [m].

$T_c=$ Temperatura del cilindro [sg].

$T_f=$ Temperatura final del aro [sg].

$A_o=$ Area inicial [m²].

$\alpha$ = Coeficiente de expansión lineal [ $\frac{1}{^oC}$ ].

$\Delta T$ = Incremento de la temperatura [ºC].

Solución:

Para hallar la temperatura final del aro, inicialmente convertiremos el valor de los diámetros a metros, luego reemplazamos la formula del área de un círculo en la formula de expansión del área y despejamos la temperatura final.

Primero:

Convertir el valor de los diámetros a metros.

Nota: El metro pertenece al sistema internacional de unidades (SI).

$50cm \times \frac{0.01m}{1cm}=0.5m$

$49.92cm \times \frac{0.01m}{1cm}=0.4992m$

Segundo:

El incremento del área es igual al área del cilindro, porque es el valor final de expansión a donde tiene que llegar el aro.

$\Delta A=A_o + 2\alpha \times A_o(T_f - T_o)$

Como podemos ver el área del aro es el área inicial en la formula.

$\Delta A_c = A_{aro} + 2\alpha \times A_{aro}(T_f - T_o)$

$\Pi \times \frac{D_c^2}{4} = \Pi \times \frac{D_{aro}^2}{4} + 2\alpha \times \Pi \times \frac{D^2}{4}(T_f - 17^oC)$

Multiplicamos toda la ecuación por (4/π) para eliminar (π/4).

$\Pi \times \frac{D_c^2}{4} \times (\frac{4}{\Pi}) = \Pi \times \frac{D_{aro}^2}{4} \times (\frac{4}{\Pi}) + 2\alpha \times \Pi \times \frac{D^2}{4}(T_f - 17^oC) \times (\frac{4}{\Pi})$