Física II – Ejercicio de Termodinámica 01 | Ney

Publicidad

Problema:

En un experimento en laboratorio los ingenieros quieren saber la temperatura en la que un cuerpo de plomo alcanza los 25.43m de longitud, cuando inicialmente se mantiene 25.34m a una temperatura de 26°C. Coeficiente de dilatación lineal del Plomo 29X10^-6°C-¹.

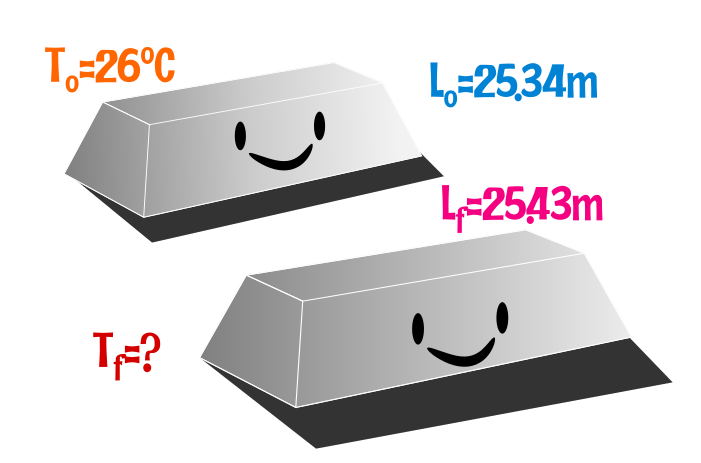
Datos:

$L_f = 25.43m$

$L_o = 25.43m$

$T_o = 26^\circ C$

$\alpha = 29\times10^-6^{\circ} C^{-1}$

Donde:

$T_o = Temperatura inicial.$

$T_f = Temperatura final.$

$L_f = Longitud$ $final.$

$L_o = Longitud$ $inicial.$

$\alpha = Coeficiente de$ $expansi\acute{o}n$ $lineal.$

$\Delta T = Incremento$ $de$ $la$ $temperatura.$

$\Delta L = Incremento$ $de$ $la$ $longitud.$

Formulas:

(1) $\Delta L = \alpha\times L_o\times \Delta T$

(2) $L = L_o\times( 1+ \alpha\times \Delta T )$

(3) $\Delta T = T_f - T_o$

Publicidad

Solución:

Reemplazamos la Formula (3) en la Formula (2) :

$L = L_o\times( 1+ \alpha\times (T_f - T_o))$

Luego $L_o$ multiplica a todo lo que esta dentro del paracentesis :

$L = L_o + L_o \times \alpha\times (T_f - T_o)$

$L_o$ esta sumando pasa al otro lado a restar :

$L - L_o= L_o \times \alpha\times (T_f - T_o)$

La $L_o$ y $\alpha$ que multiplican pasan a dividir :

$\frac{L - L_o}{L_o \times \alpha} = T_f - T_o$

La $T_o$ esta restando y pasa a sumar :

$\frac{L - L_o}{L_o \times \alpha} + T_o = T_f$

Invertimos ambos lados :

$T_f = \frac{L - L_o}{L_o \times \alpha} + T_o$

Reemplazamos los valores dados en la formula :

$T_f = \frac{25.43 - 25.34}{25.34 \times 29\times 10^{-6}} + 26$

$T_f = 148.4723077^oC$

Redondeando a dos decimales :

$T_f = 148.47^oC$

Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.

Publicidad

Relacionado

Categorías: Dilatación térmicaFísicaTermodinámica

Etiquetas: Coeficiente de dilatación lineal del plomocontoh soal pemuaian panjangejercicios de dilatación térmicaejercicios resueltos de termodinamicaLinear Lead Expansion Coefficientthermal expansion exercisesun cuerpo de plomo esta a una temperatura de 26Cun cuerpo de plomo mide 25.34 metros

Subscribe

2 Comments

Oldest

Newest Most Voted

Inline Feedbacks

View all comments

erick tirado

3 years ago

pues eso ahi daria 26 porque todo numero dividido por 0 es igual a 0 y si le sumamamos 26 eso es pues 26

0

Reply

Ney

Author

Reply to erick tirado

3 years ago

No estas tomando en cuenta los decimales.

0

Reply