Física II – Ejercicio de Mecánica de Fluidos Presión 02 | Ney

Publicidad

Problema:

Un deposito de agua de 10m de profundidad se encuentra abierto averiguar la presión en el fondo y la presión manométrica.

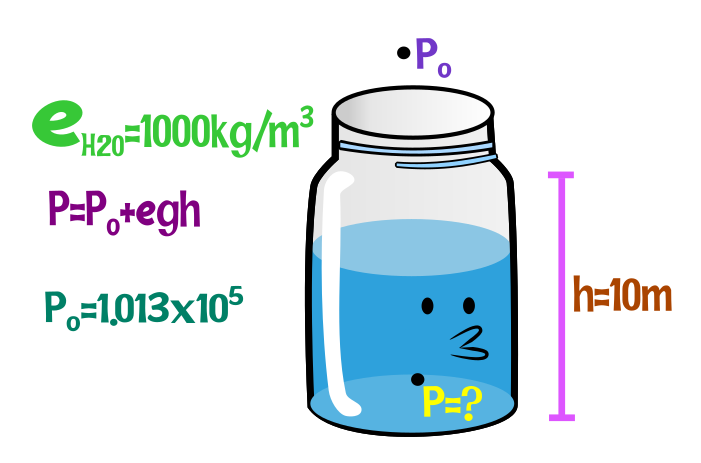
Datos:

$\varrho_{agua} = 1000\frac{kg}{m^3}$

$h = 10m$

$g = 9.8\frac{m}{s^2}$

$P_o = 1.013\times 10^5Pa$

$P - P_o = ?$

$P =?$

Donde:

$h = Altura.$

$P = Presi\acute{o}n.$

$P-P_o = Presi\acute{o}n$ $manom\acute{e}trica.$

$\varrho = Densidad.$

$g = Gravedad.$

Publicidad

$P_o = Presi\acute{o}n$ $inisializada$ $a$ $una$ $profundidad$ $cero.$

Formula:

$P = P_o + \varrho\times g \times h$

$P -P_o = \varrho \times g \times h$

Solución:

Primero hallamos la presión manométrica:

Usando la formula de la presión manométrica reemplazar los valores.

$P -P_o = \varrho_{agua} \times g \times h$

$P - P_o = 1000\frac{kg}{m^3} \times 9.8\frac{m}{s^2} \times 10m$

$P - P_o = 98000Pa$

Segundo hallamos presión en el fondo:

Usando la formula de la presión absoluta.

$P = P_o + \varrho_{agua}\times g \times h$

$P = 1.013\times10^5Pa + 1000\frac{kg}{m^3} \times 9.8\frac{m}{s^2} \times 10m$

$P = 1.99\times 10^5Pa$

Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.

Publicidad

Relacionado

Subscribe

0 Comments

Inline Feedbacks

View all comments