Física II – Ejercicio de Movimiento armónico simple| Energía 015

Publicidad

Problema:

Un bloque de masa desconocida esta esta unido a un resorte de 6.5N/m y experimenta un movimiento armónico simple con una amplitud de 10cm. Cuando el bloque está a la mitad entre su posición de equilibrio y el punto extremo, su rapidez media es 30cm/s. Calcule a) La masa del bloque b) El periodo del movimiento y c) La aceleración máxima del bloque.

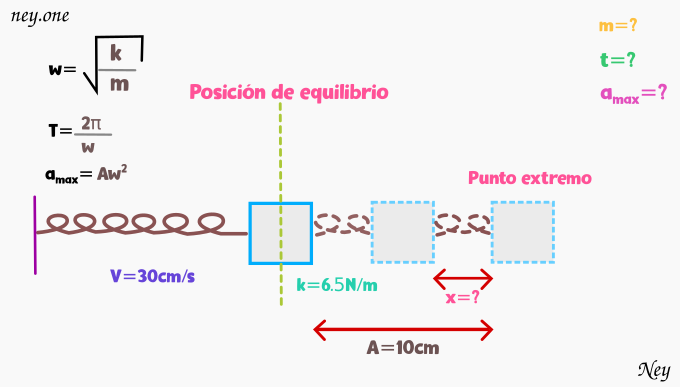
Datos:

$k=6.5N/m$

$v=30cm/s$

$A=10cm$

$m=?$

$t=?$

$a_{max}=?$

Fórmulas:

1) $\boldsymbol{ E_m=\frac{1}{2}mv^2+\frac{1}{2}kx^2 }$

2) $\boldsymbol{ \omega= \sqrt[2]{\frac{k}{m}} }$

3) $\boldsymbol{ T= \frac{2\pi}{\omega} }$

4) $\boldsymbol{ a_{max}=A\omega^2 }$

Donde:

$k$ = Constante [N/m].

$v$ = Velocidad del bloque [m/s].

$A$ =Amplitud [m].

$a_{max}$ = Aceleración máxima [m/s²].

$Em$ = Energía mecánica [J].

$\omega$ =Frecuencia angular [rad/s].

$T$ = Periodo [s].

$x$ = Distancia [m].

Solución:

Antes de empezar a resolver este problema vamos a realizar unos cálculos auxiliares de conversión de sistema de unidades.

Cálculos auxiliares:

$v=30\frac{cm}{s}$

${\Large 30\frac{\not{cm}}{s} \times \frac{0.01m}{1\not{cm}}=0.3m }$

$A=10cm$

$10\not{cm} \frac{0.01m}{1\not{cm}}=0.1m$

Ahora para resolver este problema vamos a empezar encontrando la posición del bloque. Sabemos que la amplitud es igual a A=0.1m y como el bloque esta a la mitad de la posición de equilibrio y el punto extremo, dividimos la amplitud entre 2.

$x= \frac{A}{2} = 0.05m$

Primero:

a) m=?

Para encontrar la masa del bloque usamos la fórmula de la energía mecánica 1)

$\boldsymbol{ E_m=\frac{1}{2}mv^2+\frac{1}{2}kx^2 }$

Publicidad

A esta fórmula llamaremos $E_{m1}$

$\boldsymbol{ E_{m1}=\frac{1}{2}mv^2+\frac{1}{2}kx^2 }$ …(1)

Partiendo de está fórmula (1) decimos que x=A y reemplazamos

$\boldsymbol{ E_m=\frac{1}{2}mv^2+\frac{1}{2}kA^2 }$

A esta fórmula la llamamos $E_{m2}$

$\boldsymbol{ E_{m2}=\frac{1}{2}mv^2+\frac{1}{2}kA^2 }$ …(2)

Ahora tomamos la fórmula (1) y su variante la fórmula (2) y las igualamos

$E_{m1} = E_{m2}$

$\boldsymbol{ \frac{1}{2}mv^2+\frac{1}{2}kx^2 =\frac{1}{2}mv^2+\frac{1}{2}kA^2 }$

Cuando el bloque llega al punto extremo que es la amplitud su velocidad es «0» entonces tachamos la velocidad de $E_{m2}$ .

$\boldsymbol{ \frac{1}{2}mv^2+\frac{1}{2}kx^2 =\frac{1}{2}m\not{v}^2+\frac{1}{2}kA^2 }$

$\boldsymbol{ \frac{1}{2}mv^2+\frac{1}{2}kx^2 =\frac{1}{2}kA^2 }$

Reemplazamos los valores numéricos en la igualdad

$\frac{1}{2} \times m \times 0.3^2 + \frac{1}{2} \times 6.5 \times 0.05^2 =\frac{1}{2} \times 6.5 \times 0.1^2$

Despejamos la masa

$\frac{1}{2} \times m \times 0.3^2 + 0.08125 = 0.0325$

$\frac{1}{2} \times m \times 0.3^2 = 0.0325 - 0.008125$

$\frac{1}{2} \times m \times 0.09 = 0.024375$

$m \times 0.09 = 2 \times 0.024375$

$m \times 0.09 = 0.04875$

${\large m = \frac{0.04875}{0.09} }$

$m =0.54166$

$m =0.5417kg$

Segundo:

b) t=?

Para saber cuanto tarda el bloque en su movimiento armónico simple, primero debemos encontrar el valor de la frecuencia angular.

$\boldsymbol{ \omega= \sqrt[2]{\frac{k}{m}} }$

${\large \boldsymbol{ \omega= \sqrt[2]{\frac{6.5N/m}{0.542kg}}= 3.463rad/s } }$

$T=\frac{2 \times \pi}{\omega}$

$T=\frac{2 \times \pi}{3.463}= 1.814376s$

Tercero:

c) $a_{max}=?$

Finalmente encontramos la aceleración máxima

$a_{max}=A \times \omega^2$

$a_{max}=0.1 \times 3.463^2$

$a_{max}=1.199$

$a_{max}=1.2m/s$

Publicidad

Relacionado

Categorías: FísicaMovimiento armónico simple

Tags: aceleración maxima fórmula en m.a.s.Formula de la frecuencia angularFórmula del periodo movimiento armonico simpleMovimiento armónico simple problemas resueltosMovimiento armónico simple problemas resueltos y explicados

Subscribe

1 Comment

Oldest

Newest Most Voted

Inline Feedbacks

View all comments

jose ttito

2 years ago

excelente

1

Reply