Física II – Ejercicio de Movimiento armónico simple 09

Introducción:

Ayer no logre concentrarme para redactar un nuevo post, ya que tengo muchas ideas en la cabeza y pienso en llevarlas a cambo; pero al final creo que no son tan buenas y las dejo de lado (espero retomarlas).

Pero bueno ya estamos en los primeros días de clase y en poco tiempo estaremos abrumados por exámenes y prácticos, así que mejor vamos a resolver un nuevo ejercicio.

Problema:

Un objeto de 2.5kg está unido a un muelle horizontal y realiza un movimiento armónico simple sobre una superficie horizontal sin rozamiento con una amplitud a 5cm y una frecuencia de 3.3Hz. ¿Hallar la velocidad máxima y la aceleración máxima?.

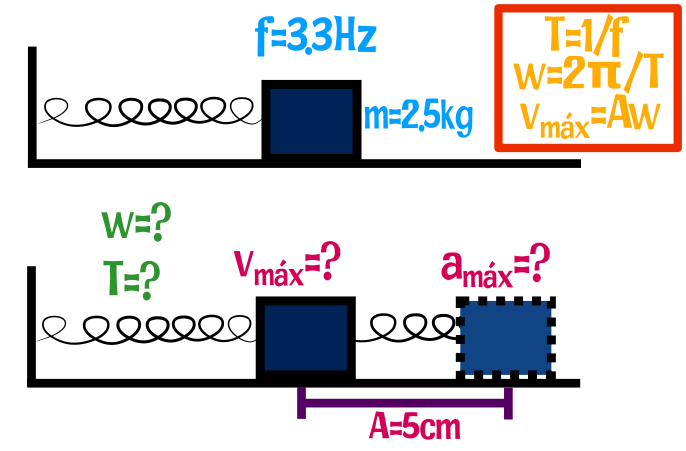
Datos:

$m=2.5kg$

$A=5cm$

$f=3.3Hz$

$v_{max}=?$

$A_{max}=?$

Formulas:

(1) $T=\frac{1}{f}$

(2) $w=\frac{2\Pi}{T}$

(3) $v_{max}=A\times w$

(4) $a_{max}= A\times w^2$

Donde:

$m=$ Masa del objeto [kg].

$A=$ Amplitud es la mayor distancia a la cual es estirado el resorte [m].

$v=$ Velocidad [m/sg]

$f=$ Frecuencia [Hz].

$w=$ Frecuencia angular [Rad/sg].

$a_{max}=$ Aceleración máxima [m/sg²].

Solución:

Si observamos un poco las formulas podremos notar que la velocidad máxima y la aceleración máxima, tienen en común la frecuencia angular en sus respectivas formulas y a su vez la frecuencia angular depende del periodo y bueno, ya sabemos por donde empezar…

Primero:

Hallamos el periodo con la formula (1) ya que tenemos como dato la frecuencia.

$T=\frac{1}{f}$

$T=\frac{1}{3.3Hz}$