Física II – Ejercicio de Movimiento armónico simple 05

Publicado por Ney en

Publicidad

Problema:

Cuatro pasajeros cuya masa combinada es de 250kg comprimen 4.00cm los resortes de un automóvil con amortiguadores vencidos cuando se suben en el. Modele el auto y los pasajeros como un solo cuerpo sobre un solo resorte ideal. Si el automóvil cargado tiene un periodo de vibración de 1.08sg. ¿Qué periodo tiene cuando está vació?.

Cuatro pasajeros cuya masa combinada es de 250kg - Movimiento anrmónico simple ejercicios resueltos (Ney)

 

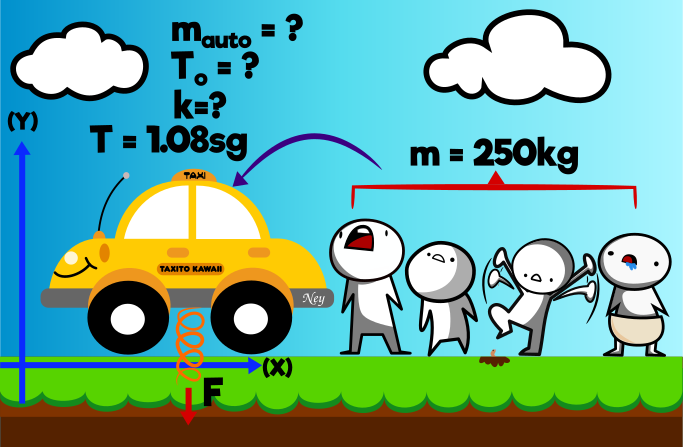
Datos:

m=250kg

T= 1.08sg

T_o=?

m_{auto}=?

k=?

Formulas:

(1) {\Large T=2\Pi \sqrt[2]{ \frac{m}{k} } }

(2) F=-k\times x

Donde:

m, m_{personas}, m_{auto}: Masas de objetos o personas [kg].

T = Periodo es el tiempo necesario para que un ciclo completo de vibración [sg].

T_o= Periodo inicial [sg].

x = Distancia es la posición del objeto que oscila en función del tiempo [m].

k = Constante elástica del muelle o resorte elástico, que relaciona fuerza y alargamiento[N/m].

w= Peso de un objeto o persona [N].

Solución:

Para este ejercicio lo primero  que podemos hacer es hallar el valor de la contaste de Hooke o la constante del resorte.

Primero:

Usando la formula (2) despejamos k y multiplicando ambos lados de la ecuación por 1/x.

F=-k \times x

F(\frac{1}{x}) =-k \times x \times (\frac{1}{x})

(\frac{F}{x}) =-k

{\Large -k=\frac{F}{x} } \times (-1)

{\Large k=-\frac{F}{x} }

Sabemos que el peso es una fuerza entonces.

F=w=m\times g

F=250kg \times 9.8\frac{m}{sg^2}

F= 2450N

Reemplazando el valor de la fuerza en la formula y también la distancia, donde 1cm=0.01m. Entonces si la distancia es 4cm en metro seria 0.04m.

{\Large k=-\frac{F}{x} }

La fuerza es negativa por que su dirección esta en el eje (-Y).

Publicidad

{\Large k=-\frac{-2450N}{0.04m} }

{\Large k=61250\frac{N}{m} }

Segundo:

Sabemos que la masa total es la masa de las personas mas la masa del auto, entonces reemplazamos la masa total en la formula (2), para hallar la masa del auto.

{\Large m_t= m_{auto}+m_{personas} }

{\Large T=2\Pi \sqrt[2]{ \frac{m}{k} } }

donde m=m_t entonces.

{\Large T=2\Pi \sqrt[2]{ \frac{m_t}{k} } }

{\LARGE T=2\Pi \sqrt[2]{ \frac{m_{auto}+m_{personas}}{k} } }

Ahora si despejamos la masa del auto.

{\LARGE \frac{T}{2\Pi}= \sqrt[2]{ \frac{m_{auto}+m_{personas}}{k} } }

{\LARGE (\frac{T}{2\Pi})^2 = \frac{m_{auto}+m_{personas}}{k} }

{\LARGE (\frac{T}{2\Pi})^2 \times k = m_{auto}+m_{personas} }

{\LARGE (\frac{T}{2\Pi})^2 \times k - m_{personas} = m_{auto} }

{\LARGE m_{auto} = (\frac{T}{2\Pi})^2 \times k - m_{personas} }

Momento de reemplazar los valores para hallar la masa del auto.

{\LARGE m_{auto} = (\frac{1.08sg}{2\Pi})^2 \times 61250\frac{N}{m} - 250kg }

{\LARGE m_{auto} = 1559.6kg}

Tercero:

Hallamos el periodo inicial cuando al auto  esta vació.

{\Large T=2\Pi \times \sqrt[2]{ \frac{m_t}{k} } }

{\Large T=2\Pi \times \sqrt[2]{ \frac{m_{auto}}{k} } }

{\Large T=2\Pi \times \sqrt[2]{ \frac{1559.6kg}{61250\frac{N}{m}} } }

Recordemos que 1N=kg *m/s², entonces reemplazamos 1N por su equivalencia.

{\Large T=2\Pi \times \sqrt[2]{ \frac{1559.6kg}{61250\frac{\frac{kg \times m}{sg^2}}{m}} } }

Dividimos y simplificamos.

{\Large T=2\Pi \times \sqrt[2]{0.025462857sg^2} }

{\Large T=2\Pi \times \sqrt[2]{0.025462857}\times \sqrt[2]{sg^2} }

{\Large T=2\Pi \times 0.159570852sg }

{\Large T=1.002613237sg }

Redondeando a tres decimales.

{\Large T=1.003sg }

Conclusión: El periodo inicial cuando el auto esta vació es $latex1.003sg$.

Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.

Publicidad

Categorías: FísicaMovimiento armónico simple
Tags:
Subscribe
Notify of
guest

9 Comments
Oldest
Newest Most Voted
Inline Feedbacks
View all comments
Fani

Por que al momento de despejar la masa del auto K la pasas dividiendo?

0
Reply
Ney

Por que, me equivoque en realidad k (la constante) pasa a multiplicar al otro lado de la ecuación, ya lo corregí.

0
Reply
Dani

Porque pones el 250kg al reemplazarlo en la masa de las personas si es la masa total?

1
Reply
Ney

250kg es la masa de todas las personas y la masa total es la suma de la masa del auto y de las personas; por otro lado ya revise el ejercicio y no veo error al reemplazar (en su lugar encontré la la gravedad elevada al cuadrado en lugar del segundo).
Si pudieras decirme de forma más especifica a que parte te refieres, entonces te podría ayudar con la duda.

1
Reply
Daniela Tola Gaspar

Muy buena explicación

1
Reply
Ney

¡Muchas gracias, me alegraste el día!😀😃😄😇

2
Reply
David

Conclusión se escribe con s

0
Reply
Ney

Tienes razón ya lo corregi, a menudo confundo la «c» con la «s».

0
Reply
paúl

la fórmula del periodo no seria 2pi por la raiz de k/m?? tu le pones m/k

0
Reply

Entradas relacionadas

Física

Concepto de física

Publicidad ¿Qué es física? Podemos definir a la física como una rama de la ciencia que se encarga de estudiar y observar los fenómenos, algunos de ellos son: la energía, las fuerza, gravedad, el movimiento, Leer más…

Física

Ejercicio de Movimiento armónico simple| Energía 016

Publicidad Problema: Un objeto se mueve en movimiento armónico simple con periodo de 0.8s y aceleración máxima de 6.5m/s². Calcule su rapidez máxima. Datos: Fórmulas: 1) 2) 3) Donde: = Constante [N/m]. = Velocidad del Leer más…

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015

Publicidad Problema: Un bloque de masa desconocida esta esta unido a un resorte de 6.5N/m y experimenta un movimiento armónico simple con una amplitud de 10cm. Cuando el bloque está a la mitad entre su Leer más…