Física II – Ejercicio de Movimiento armónico simple 03 | Ney

Publicidad

Problema:

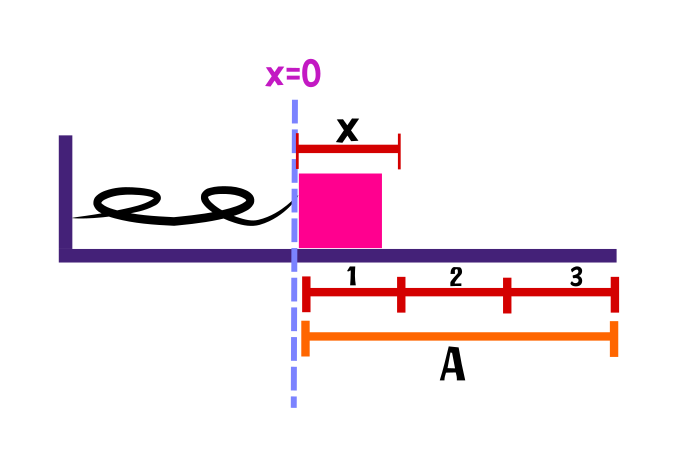
Un oscilador armónico se encuentra en un instante determinado en una posición que es igual a un tercio de su amplitud A. Determina para dicho instante la relación existente entre la energía cinética y la energía potencial (Ec/Ep ).

Datos:

$\frac{A}{3}$

Formulas:

(1) $E_c=\frac{1}{2}k(A^2 - x^2)$

(2) $E_p=\frac{1}{2}k\times x^2$

Donde:

$A=$ Amplitud o elongación máxima[m].

$x=$ Distancia, representa la posición del objeto que oscila en función del tiempo [m].

$k=$ Constante elástica del muelle, que relaciona fuerza y alargamiento [N/m].

$E_c=$ Energía cinética [J].

$E_p=$ Energía potencial [J].

Solución:

Como la distancia a la que se encuentra el oscilador armónico es un tercio de la amplitud esta sera entonces la distancia para la energía potencial y cinética.

Primero:

$x=\frac{A}{3}$

Reemplazamos el valor de la distancia en la formula de la energía cinética.

Publicidad

$E_c=\frac{1}{2}k(A^2 - x^2)$

$E_c=\frac{1}{2}\times k \times(A^2 - \frac{A^2}{3^2})$

$E_c=\frac{1}{2} \times k \times(\frac{9A^2 - A^2}{9})$

$E_c=\frac{1}{2}k(\frac{8A^2}{9})$

Segundo:

Para hallar la relación entre la energía potencial y la energía cinética las dividiremos.

${\LARGE \frac{E_c}{Ep}}$

${\LARGE \frac{\frac{1}{2}k(\frac{8A^2}{9})}{\frac{1}{2}k \times x^2}}$

${\huge \frac{\frac{1}{2}\times k \times (\frac{8A^2}{9})}{\frac{1}{2}k \times x^2}}$

El valor de un tercio de la amplitud también aplica en la energía potencial.

${\LARGE \frac{\frac{1}{2}k(\frac{8A^2}{9})}{\frac{1}{2}k\times (\frac{A}{3})^2}}$

${\LARGE \frac{\frac{1}{2}k(\frac{8A^2}{9})}{\frac{1}{2}k\times (\frac{A^2}{9})}}$

Multiplicamos medios con extremos.

${\LARGE \frac{2\times 3\times 1k\times A^2}{1k\times 8\times A^2\times 2\times 9}}$

Simplificamos k, A,dos y nueve.

${\LARGE \frac{1k\times 8\times A^2\times 2\times 9}{2\times 9\times 1k\times A^2}} = 8$

Conclusión: La relación entre Ec. y Ep. es ocho.

Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.

Publicidad

Relacionado

Categorías: FísicaMovimiento armónico simple

Tags: A harmonic oscillator is at a certain moment in a position that is equal to one third of its amplitude AGráfico de un oscilador armónicoGraph of a harmonic oscillatorunidad de medida de la energía cineticaunidad de medida de la energía potencialunit of measure of potential energyunit of measurement of kinetic energy

Subscribe

0 Comments

Inline Feedbacks

View all comments