Física II – Ejercicio de Movimiento armónico simple 014 | Ney

Publicidad

Problema:

El desplazamiento en función del tiempo de una masa de 1.50kg en un resorte está dado por la ecuación.

$x(t) = 8.2cm \cos (4.2s^-1t - 2.42)$

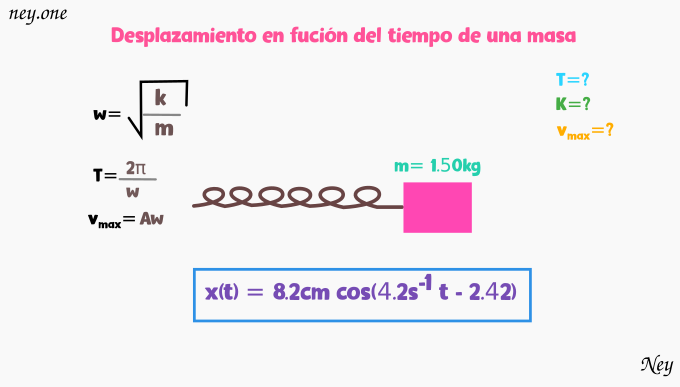
Calcule:

a) El tiempo que tarda una vibración completa.

b) La constante de la fuerza del resorte

c) La rapidez máxima de la masa.

Datos:

$A= 8.2cm$

$\omega = 4.2s$

$\phi= 2.42$

$T=?$

$k=?$

$v_{max}=?$

Fórmulas:

(1) $T= \frac{2\pi}{\omega}$

(2) $\omega = \sqrt[2]{ \frac{k}{m}}$

(3) $v_{max}= A \times \omega$

Donde:

$A =$ Amplitud [m].

$\omega =$ frecuencia angular [rad/s].

$\phi =$ fi.

$T=$ Tiempo [s].

$v_{max}=$ velocidad máxima [m/s].

$k =$ constante.

$m =$ masa [kg]$

Aclaración: Los datos salen de la comparación de la ecuación que tenemos y la siguiente fórmula de desplazamiento en M.A.S.

$x(t) = 8.2cm \cos (4.2s^{-1}t - 2.42)$

$x = A \cos (\omega t + \phi)$

Publicidad

entonces concluimos que: $A= 8.2cm$ , $\omega = 4.2s$ etc…

Solución:

Primero:

Encontramos el tiempo que tarda la vibración completa

$T= \frac{2\pi}{\omega}$

$T= \frac{2\pi}{4.2s}$

$T= 1.49s$

Redondeando

$T= 1.5s$

Segundo:

De la fórmula (2) despejamos la constante (k)

$\omega = \sqrt[2]{ \frac{k}{m}}$

$\omega^2 = \frac{k}{m}$

$\omega^2 \times m= k$

$k = \omega^2 \times m$

$k = 4.2^2 \times 1.50$

$k = 26.46\frac{N}{m}$

Tercero:

$A= 8.2cm$

Convertimos 8.2cm a metros

$8.2cm \times \frac{0.01m}{1cm} =0.082m$

Finalmente encontramos la rapidez máxima de la masa

$v_{max}= A \times \omega$

$v_{max}= 0.082m \times 4.2s$

$v_{max}= 0.344\frac{m}{s}$

Conclusión:

Encontramos todas las 3 incógnitas:

a) El tiempo que tarda una vibración completa $T= 1.5s$ .

b) La constante de la fuerza del resorte $k = 26.46\frac{N}{m}$ .

c) La rapidez máxima de la masa $v_{max}= 0.344\frac{m}{s}$ .

Publicidad

Relacionado

Categorías: FísicaMovimiento armónico simple

Etiquetas: ejercicios resueltos m.a.s.Problemas resueltos de movimiento armonico simple

Subscribe

0 Comments

Inline Feedbacks

View all comments