Física II – Ejercicio de Movimiento armónico simple 013 | Ney

Publicidad

Problema:

Un alambre colgante tiene 2 m de longitud. Cuando una bola de acero de 80kg se suspende del alambre, este se estira 2mm. Si se tira de la bola hacia abajo una distancia adicional pequeña y se la suelta. ¿Con que frecuencia vibrara?

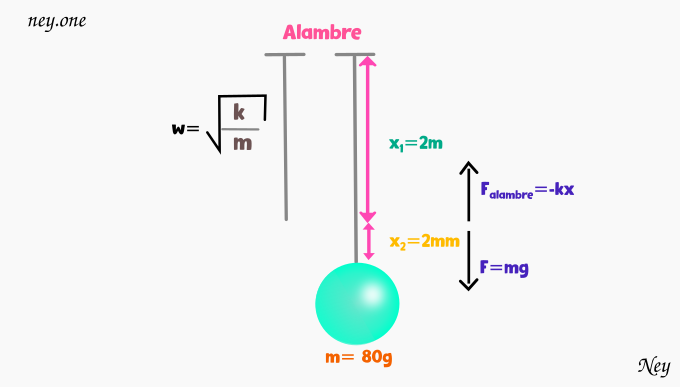
Datos:

$x_{1} = 2 m$

$m = 80 kg$

$x_{2}= 2 mm$

$f= ?$

Fórmulas:

(1) ${\Large F = -k \times x }$

(2) ${\Large \omega = \sqrt[2]{\frac{k}{m} }}$

(3) ${\Large f= \boldsymbol{\frac{\omega} {2\pi}} }$

Donde:

$x_{1}=$ Longitud inicial [m].

$m =$ masa de la bola [kg].

$x_{2}=$ Longitud final [m].

$f =$ Frecuencia [Hz].

Solución:

Para este problema lo primero que vamos a necesitar es encontrar la constante $k$ , luego la frecuencia angular $\omega$ y con la frecuencia angular encontramos la frecuencia $f$ .

Calculo auxiliar:

$2 mm \times \frac{0.001m}{1mm} = 0.002m$

Primero:

Despejamos k de la formula (1)

Publicidad

${\Large F = -k \times x }$

${\Large \frac{F}{x} = -k}$

Invertimos la ecuación

${\Large -k = \frac{F}{x}}$

La fuerza es igual a la masa por gravedad, entonces reemplazamos

$F = m \times g$

${\Large \boldsymbol{-k = \frac{F}{x}}}$

${\Large \boldsymbol{-k = \frac{m \times g}{x}}}$

Ahora reemplazamos los datos en la fórmula

${\Large \boldsymbol{-k = \frac{80kg \times 9.8\frac{m}{s^2}}{0.002m}}}$

${\Large -k = 392000\frac{N}{m} }$

Segundo:

Obtenemos la frecuencia angular

${\Large \omega = \sqrt[2]{\frac{k}{m} }}$

${\Large \omega = \sqrt[2]{\frac{ 392000}{80} }}$

${\Large \omega = 70\frac{rad}{s} }$

Tercero:

Como ya tenemos la frecuencia angular pasamos a hallar la frecuencia

${\Large f= \boldsymbol{\frac{\omega} {2\pi}} }$

${\Large f= \boldsymbol{\frac{70} {2\pi}} }$

${\Large f= 11.14Hz }$

Redondeando

${\Large f= 11Hz }$

Publicidad

Relacionado

Categorías: FísicaMovimiento armónico simple

Tags: Movimiento armónico simple ejercicios resueltos

Subscribe

1 Comment

Oldest

Newest Most Voted

Inline Feedbacks

View all comments

VÍCTOR MARTEL MARTÍNEZ

1 year ago

excelentes explicaciones!! clarísimo!!

0

Reply