Introducción:
Llevo un día y medio sin pc y a pesar de que estoy floja, creo que es el momento de resolver nuevamente otro ejercicio de física y como no tengo nada más que agregar comencemos.
Problema:
Una partícula ejecuta un movimiento armónico simple con una amplitud de 4.00cm. su posición es de x=2.6cm y x=-2.6cm. Cuando su rapidez es igual a la mitad de su rapidez máxima.
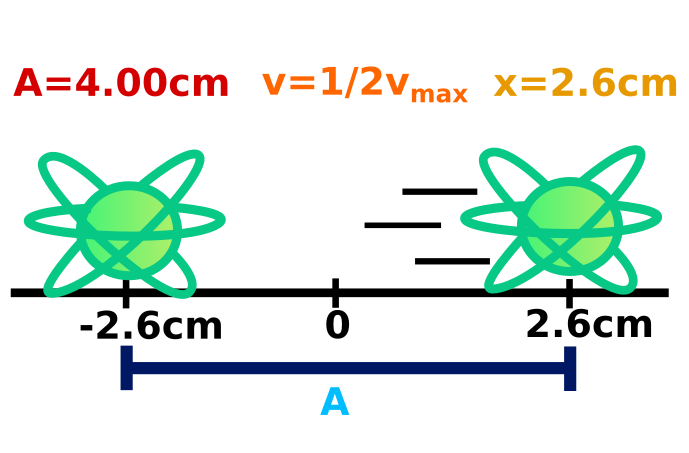
Datos:
Formulas:
(1) 
(2) ![v=W\times\sqrt[2]{A^2-x^2}](https://s0.wp.com/latex.php?latex=v%3DW%5Ctimes%5Csqrt%5B2%5D%7BA%5E2-x%5E2%7D&bg=ffffff&fg=000&s=0&c=20201002)
Donde:
Amplitud es la magnitud máxima del desplazamiento con respecto al equilibrio [m].
Distancia es la posición del objeto que oscila en función del tiempo [m].
Peso es la fuerza con que la Tierra atrae a un cuerpo [N].
Velocidad [ m/s].
Solución:
En el problema podemos leer que la rapidez es igual a la mitad de su rapidez máxima. Entonces igualaremos la formula uno y dos.
Primero:
Igualando (1) y (2)
(1)
(2)
![W\times\sqrt[2]{A^2-x^2}=A\times W](https://s0.wp.com/latex.php?latex=W%5Ctimes%5Csqrt%5B2%5D%7BA%5E2-x%5E2%7D%3DA%5Ctimes+W&bg=ffffff&fg=000&s=0&c=20201002)
Como la velocidad es solo la mitad de la velocidad máxima, multiplicamos la velocidad máxima por (1/2).
![W\times\sqrt[2]{A^2-x^2}=(\frac{1}{2})A\times W](https://s0.wp.com/latex.php?latex=W%5Ctimes%5Csqrt%5B2%5D%7BA%5E2-x%5E2%7D%3D%28%5Cfrac%7B1%7D%7B2%7D%29A%5Ctimes+W&bg=ffffff&fg=000&s=0&c=20201002)
De la fracción (1/2) el dos pasa a multiplicar y el uno a dividir.
![2\times W \times\sqrt[2]{A^2-x^2}=A\times W](https://s0.wp.com/latex.php?latex=2%5Ctimes+W+%5Ctimes%5Csqrt%5B2%5D%7BA%5E2-x%5E2%7D%3DA%5Ctimes+W&bg=ffffff&fg=000&s=0&c=20201002)
La frecuencia angular pasa a dividir.
![\Large{ \frac{2\times W \times\sqrt[2]{A^2-x^2}}{W}=A}](https://s0.wp.com/latex.php?latex=%5CLarge%7B+%5Cfrac%7B2%5Ctimes+W+%5Ctimes%5Csqrt%5B2%5D%7BA%5E2-x%5E2%7D%7D%7BW%7D%3DA%7D&bg=ffffff&fg=000&s=0&c=20201002)
![\Large{ 2\times\sqrt[2]{A^2-x^2}=A}](https://s0.wp.com/latex.php?latex=%5CLarge%7B+2%5Ctimes%5Csqrt%5B2%5D%7BA%5E2-x%5E2%7D%3DA%7D&bg=ffffff&fg=000&s=0&c=20201002)
La raíz se va con los exponentes.
La amplitud es simplificada y la distancia pasa al otro lado con signo positivo.
Conclusión:
Cuando la velocidad o la rapidez es la mitad de la velocidad máxima, su distancia es 2cm, entonces la respuesta es la opción falso.
Si encuentras algún error o algún otro detalle que se me hubiera escapado por favor dejalo en los comentarios, para que pueda rectificarlo.
