Problema:
Una muestra de mineral pesa 17.50N en el aire; pero si se cuelga de un hilo ligero y se sumerge por completo en agua, la tensión en el hilo es de 11.20N. Calcule el volumen total de la muestra.
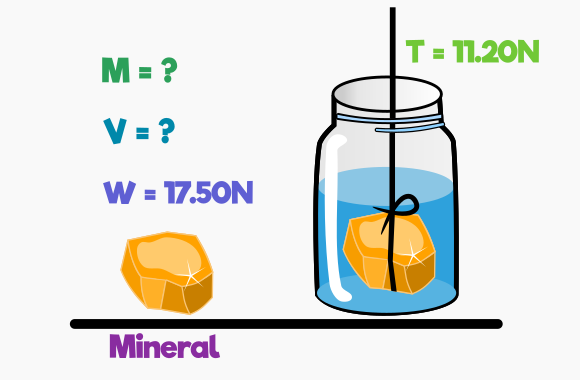
Datos:
Formulas:
(1)
(2)
(3)
Donde:
Peso [m \times g].
Tensión [N].
Volumen [m³].
Masa [kg].
Densidad [kg/m³].
Fuerza de empuje [N].
Gravedad [m/s²].
Solución:
Comenzamos hallando la maza del mineral, para ello dividimos el peso del mineral entre la gravedad.
Primero:
Usamos la formula 2 y despejamos la masa.
Reemplazamos los valores del peso y gravedad.
Segundo:
Debemos conocer a que es igual la fuerza de empuje (B), para ellos usamos las formulas 1 y 3.
(1)
(3)
De la formula 3 despejamos la masa.
Reemplazamos la masa en la formula 1.
Sabemos que el volumen corresponden al agua desalojada por el mineral y la densidad es la densidad del agua dulce.
Tercero:
Hacemos un diagrama para visualizar las fuerzas que actúan en el eje «y», para luego hacer sumatoria de fuerzas.
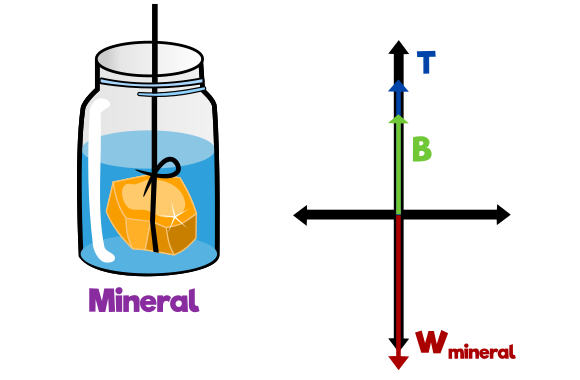
Reemplazamos las variables de cada fuerza, por las equivalencias que encontramos anteriormente.
Despejamos el volumen.
Nota: El volumen del agua desalojado es igual al volumen del objeto completamente sumergido.
Para un mayor conocimiento del principio de Arquímedes clic aquí.
El objeto sumergido en este caso es el mineral, entonces cambiamos el subíndice del volumen.
Reemplazamos los valores de la masa, la densidad y la gravedad.
Aplicando notación científica.
Conclusión:
El volumen total de la muestra de mineral es: .
Si encuentras algún error o algún otro detalle que se me hubiera escapado🤯 por favor dejalo en los comentarios, para que pueda corregirlo.


