Física II – Ejercicio de Gravitación 04

Problema:

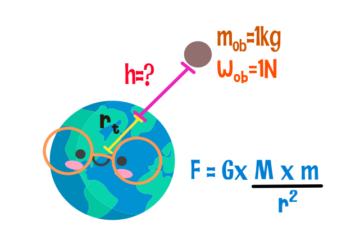
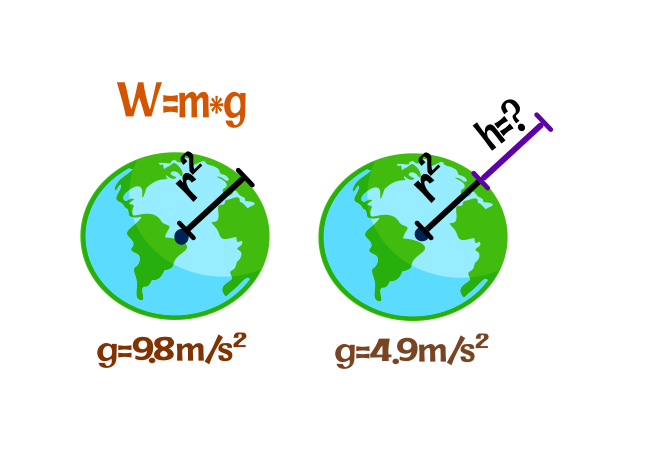
¿A qué distancia sobre la superficie terrestre la aceleración debido a la gravedad es de 4.9m/s²?, si en la superficie tiene una magnitud de 9.80 m/s² y el radio de la tierra es 6.37×10⁶m.

Datos:

$h = ?$

$g_h = 4.9\frac{m}{s^2}$

$g_o = 9.8\frac{m}{s^2}$

$r = 6.37\times 10^6m$

Donde:

$W =$ Peso [kg*m/s2].
$F =$ Módulo de la fuerza gravitatoria [N].
$m, M =$ Masas [kg].
$r =$ Distancia de separación [m].
$G =$ Constante de gravitación universal [N*m²/kg²].
$g_o, g_h =$ Gravedad [m/s²].
$r_t=$ Radio de la tierra.
$h =$ Altura[m].

Formulas:

(1) $F = G\times \frac{M \times m}{r^2}$

(2) $g = G\times\frac{m_t}{r_t^2}$

(3) $W= m\times g$

Solución:

Para hallar la distancia de la altura, en la cual la gravedad es 4.9m/s² usaremos las formulas (1) y (3). Donde el peso es igual a la masa por gravedad, entonces el peso es una fuerza y lo reemplazamos en la formula (1), posteriormente despejamos la gravedad.

Primero:

Reemplazamos el peso en la fuerza.

$W= m\times g$

$F = G\times \frac{M \times m}{r^2}$

$m\times g_o = G\times \frac{M \times m}{r^2}$

Como tenemos masa en los estrenos multiplicamos todo por 1/m.

$\Large m\times g_o = G\times \frac{M \times m}{r^2}$ $\times (\frac{1}{m})$

$g_o = G\times \frac{M}{r^2}$

Segundo:

Cuando pasemos a multiplicar el radio nos queda la siguiente igualación.

(4) $g_o \times r^2 = G\times M$

Partiendo de la ecuación (4) obtenemos la ecuación (5). Donde la masa en la formula que nos queda es la masa de la tierra y al radio de la tierra le sumamos la altura en la que la gravedad es 4.9m/s², mientras que la gravedad es 4.9m/s² eso nos da la segunda ecuación.

(5) $g_h \times (r+ h)^2 = G\times M_t$