Física II – Ejercicio de Gravitación 02 | Ney

Publicidad

Introducción:

Hola, hoy les traigo un ejercicio es muy sencillo como podrán ver más adelante, yo lo resolví como parte de mi practico de gravitación (el cual me pareció muy interesante por que me hace recordar la serie Star Trek), espero que les sea útil para practicar.

Problema:

En el punto A(2,0) se situá una masa de 2kg y en el punto B(5,0) se coloca otra masa de 4kg. Calcular la fuerza resultante que actuá sobre una tercera masa de 5kg cuando se coloca en el origen de coordenadas.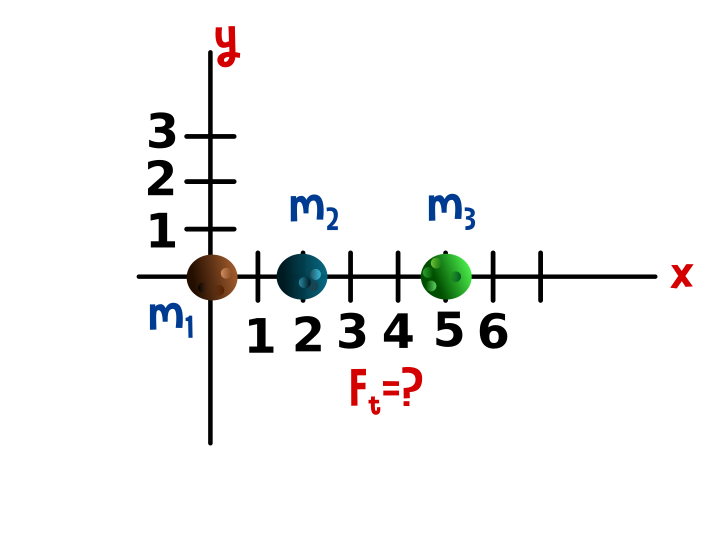

Datos:

$m_1= 5kg$

$m_2= 2kg$

$m_3 = 4kg$

$r_1 = 2$

$r_2 = 4$

$G = 6.67\times 10^{-11}N\times \frac{m^2}{kg^2}$

Donde:

$F =$ Módulo de la fuerza gravitatoria [N].
$m_1, m_2, m_3 =$ Masas de los cuerpos [kg].
$r =$ Distancia de separación [m].
$G =$ Constante de gravitación universal [N·m²/kg²].

Formulas:

$F = G\times \frac{m_1 \times m_2}{r^2}$

$F_t = F_1 + F_2$

Solución:

Debemos hallar la fuerza gravitacional que ejercen las masas $m_2$ y $m_3$ sobre la masa $m_1$ , luego la suma de ambas fuerzas gravitacionales es la fuerza resultante que actuá sobre la masa $m_1$ .

Primero:

Hallamos la fuerza gravitacional entre $m_1$ y $m_2$ .

Publicidad

$F = G\times \frac{m_1 \times m_2}{r^2}$

$F_1 = G\times \frac{m_1 \times m_2}{r_2^2}$

$F_1 = 6.67\times 10^{-11}N\times \frac{m^2}{kg^2}\times \frac{5kg\times 2kg}{2^2}$

$F _1= 1.6675\times 10^{-10}N$

Segundo:

Hallamos la fuerza gravitacional entre $m_1$ y $m_3$ .

$F = G\times \frac{m_1 \times m_2}{r^2}$

$F_2 = G\times \frac{m_1 \times m_3}{r_3^2}$

$F _2 = 6.67\times 10^{-11}N\times \frac{m^2}{kg^2}\times \frac{5kg \times 4kg}{5^2}$

$F_2 = 5.336\times10^{-11}N$

Tercero:

Sumamos la fuerzas $F_1$ y $F_2$ .

$F_t = F_1 + F_2$

$F_t = 1.6675\times 10^{-10}N + 5.336\times10^{-11} N$

$F_t = 2.2011\times10^{-10}N$

Expresando el valor con 2 decimales:

$F_t = 2.20\times10^{-10}N$

Conclusión:

La fuerza resultante que actuá sobre la tercera masa es $2.20\times 10^{-10} N.$

Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.

Publicidad

Relacionado

Categorías: Gravitación

Tags: ¿Cuanto vale la constante de gravitación?Constante de gravitación universalejemplo de la ley de gravitación universal de newtonEjercicio de gravitación resueltoejercicios de gravitación universalel eje de coordenadas donde se encuentran tres masasformula de la fuerza gravitacionalfuerza de atraccion gravitacional formulaGravitational Force Modulegravitational pull force formulaHallar la fuerza que actua sobre la masa 1Hallar la fuerza resultante que actua sobre una 3 masaMódulo de la fuerza gravitatorianewton’s law of universal gravitation exampleUnidad de medida de la fuerza gravitacionalUniversal gravitation constantuniversal gravitation exercises

Subscribe

0 Comments

Inline Feedbacks

View all comments