Física II – Ejercicio de Mecánica de Fluidos Presión 01 | Ney

Publicidad

Problema:

Un lago está cubierto con una capa de hielo de 2.75 m de espesor. Calcule la presión absoluta y la presión manométrica a una profundidad de 5.50 m en el lago. La densidad del hielo es 920 kg/m³, la densidad del agua es 1000 kg/m³y presión atmosférica es igual a1.013X10⁵Pa.

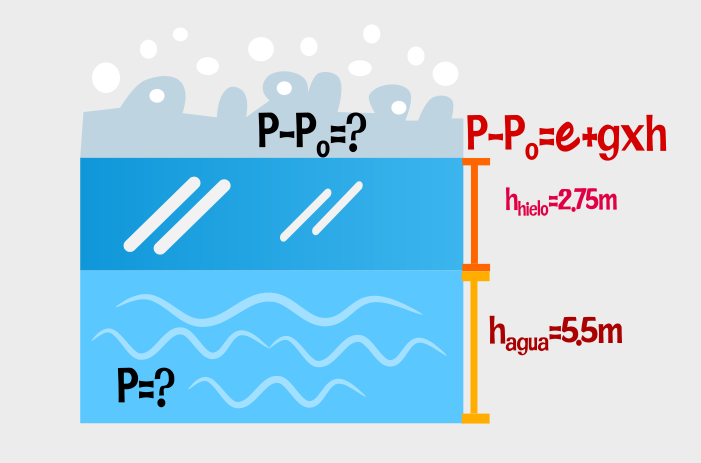
Datos :

$h_{hielo} = 2.75m$

$h{profundidad}= 5.50m$

$P = ?$

$P-P_o =?$

$\varrho_{hielo} = 920\frac{kg}{m3}$

$\varrho_{agua} = 1000\frac{kg}{m3}$

$P_o = 1.013\times 10^5Pa$

Donde :

$h$ = Altura.

$P$ = Presión.

$P-P_o$ = Presión manométrica.

$\varrho$ = Densidad.

$g$ = Gravedad.

$P_o$ = Presión inicial a una profundidad cero o presión atmosférica.

Formulas :

$P = P_o + \varrho \times g \times h$

$P -P_o = \varrho \times g \times h$

Solución :

Inicialmente podemos hallar la altura del agua:

Publicidad

hacemos la diferencia entre la profundidad del agua del lago y la altura del hielo.

$h_{agua} = h_{profundidad} - h_{hielo}$

$h_{agua} = 5.50m -2.75m$

$h_{agua} = 2.75m$

Luego, reemplazamos la altura del hielo (que resulto ser la misma que la del agua) en la formula de la presión junto con los demás datos .

Hallamos la presión el el hielo:

$P = P_o + \varrho_{hielo} \times g \times h$

$P = 1.013\times 10^5Pa + 920\frac{kg}{m^3} \times 9.8\frac{m}{sg^2} \times 2.75m$

$P = 126094Pa$

También, hallamos la presión en el agua:

$P = P_o + \varrho_{agua} \times g \times h$

$P = 126094 + 1000\frac{kg}{m^3}\times 9.8\frac{m}{sg^2} \times 5.50m$

$P = 179994Pa$

Hallamos la presión manométrica:

$P = 1.8\times 10^5Pa$

$P - P_o = \varrho_{hielo} \times g \times h_{hielo} + \varrho_{agua} \times g \times h_{profundidad}$

$P - P_o =920\frac{kg}{m^3}\times 9.8\frac{m}{sg^2}\times 2.75 + 1000\frac{kg}{m^3}\times 9.8\frac{m}{sg^2}\times 5.50m$

$P - P_o = 24794 + 53900$

$P - P_o = 78694Pa$

Expresándolo en notación científica:

$P - P_o = 7.9\times10^4Pa$

Si encuentras algún error por favor dejalo en los comentarios, para que pueda rectificar el ejercicio.

Publicidad

Relacionado

Subscribe

0 Comments

Inline Feedbacks

View all comments