Física I – Ejercicio de vectores 10 (Sears – Zemansky)

Problema:

En un vuelo de entrenamiento, una piloto estudiante vuela de Lincoln, Nebraska, a Clarinda,
Iowa; luego a St. Joseph, Missouri y después a Manhattan, Kansas. Las direcciones se
muestran relativas al norte: 0º es norte, 90º es este, 180º es sur y 270º es oeste. Use el método de componentes para calcular a) la distancia que debe volar para regresar a Lincoln desde Manhattan; y b) la dirección (relativa al norte) que debe seguir. Ilustre su solución con un diagrama vectorial.

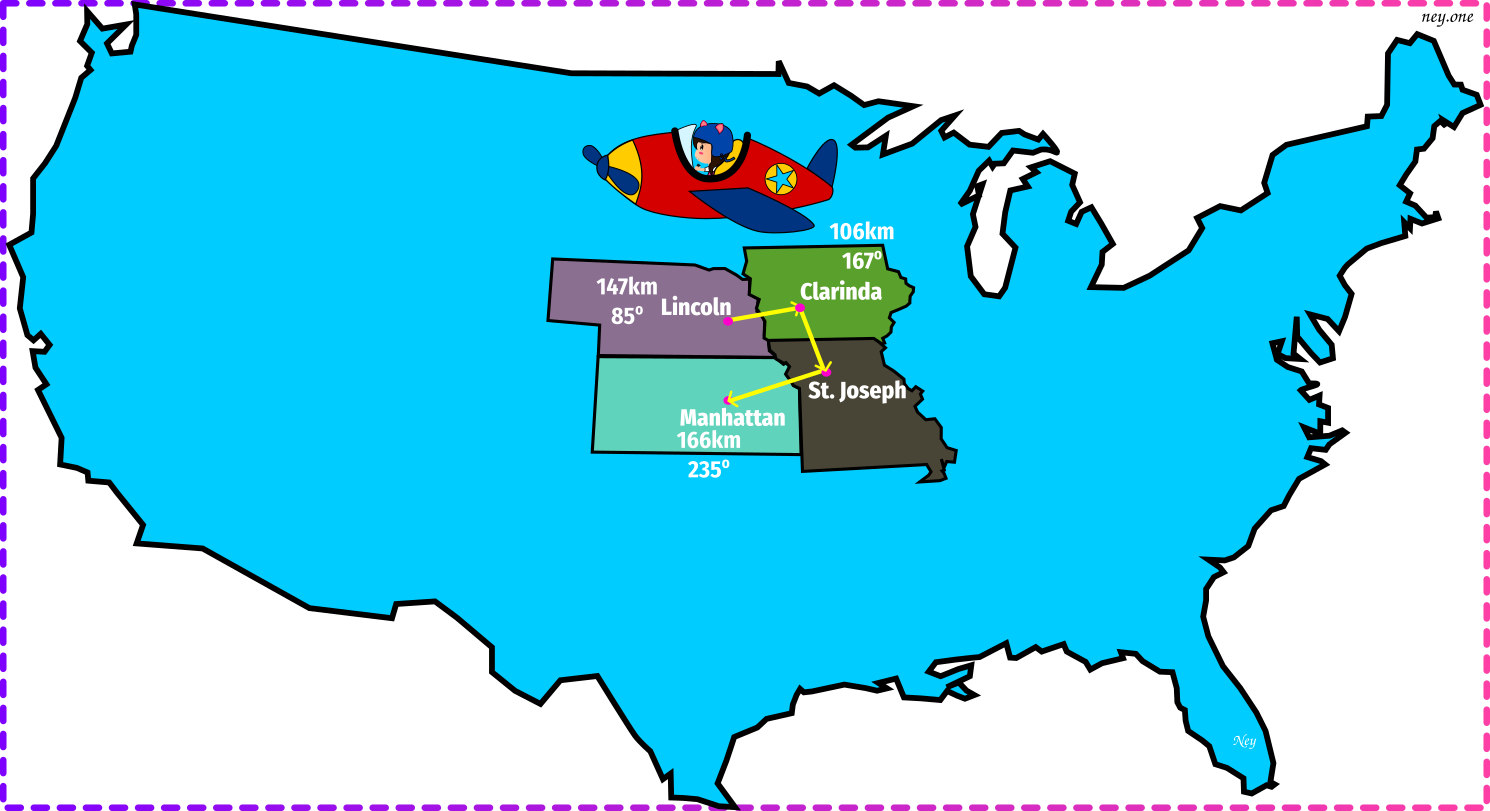
Datos:

Fórmulas:

Donde:

Solución:

Bien, el problema indica que tenemos que resolverlo con el método de componentes. Y bueno el método de componentes consiste en  qué a partir de los componentes en X y Y encontramos el vector que necesitamos.

A partir de los vectores que nos dan en la figura vamos a descomponerlos y sumarlos,  los componentes en el eje X por un lado y todos los componentes en el eje Y por el otro. La suma de estos componentes son y que son los componentes del vector que va desde Manhattan a Lincoln.

Primero:

Obtenemos el componente del vector .

Segundo:

Obtenemos el componente del vector .

Tercero:

Encontramos la distancia del vector que va desde Manhattan a Lincoln con la fórmula de Pitágoras.

Cuarto:
Ahora solo falta encontrar la dirección o ángulo del vector

Despejamos el ángulo de (gamma) y reemplazamos valores.

A   le restamos

Conclusión:

Con el metodo de componentes encontramos los componentes y , con la fórmula de Pitágoras encontramos la distancia y con la fórmula de la tangente encontramos la dirección.