Problema:
Una espeleóloga esta explorando una cueva y sigue un pasadizo 180 m al oeste, luego 210 m 45º al este del sur, y después 280 m 30º al este del norte. Tras un cuarto desplazamiento no medido, vuelve al punto inicial. Con un diagrama a escala determine la magnitud y la dirección del cuarto desplazamiento.
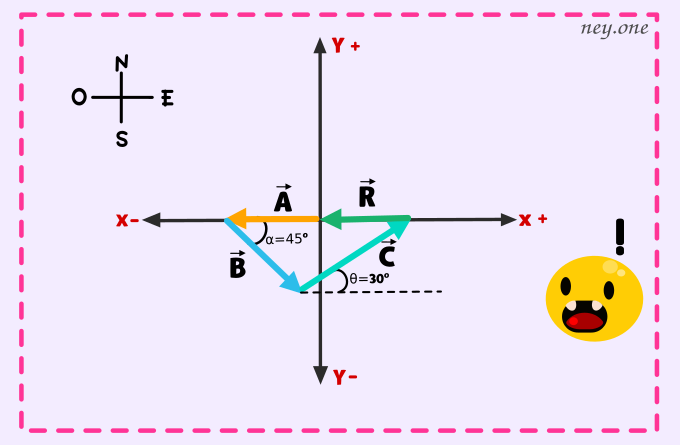
Datos:
Fórmulas:
Donde:
Solución:
Para resolver este problema vamos a encontrar los vectores componentes del vector resultante.
Como ya tenemos los vectores componentes, ahora hallamos el vector resultante
Y finalmente encontramos el ángulo de la resultante
El vector apunta hacia el sur del oeste.
Conclusión:
El resultado de este ejercicio discrepa del resultado del libro Sears-Zemansky vol. 1, al principio dude de mi respuesta; pero luego de revisarlo varias veces y comprobarlo de forma gráfica llegue a la conclusión de que el resultado del libro esta equivocado.
Esto no es nada raro a menudo se cometen errores en los libros que suelen ser corregidos en nuevas ediciones.
Cuando utilizaste el Angulo de 30 grados tenias que poner sin porque sale desde el eje y
esta mal, estas calculando la suma de los vectores abc y te falta calcular el tamaño de R
R= Las componentes en «x» y «y» de a, b, c.
Rx= ax + bx + cx… y Ry es igual a:
Ry= ay + by + cy… entonces R es igual a:
R= √(Rx+ Ry)
Si aún tienes dudas puedes ver un ejemplo similar abajo ó «puedes leer un libro de física de forma muy atenta revisando y probando todo lo que este en el libro«.
Aquí el ejemplo, dale clic
Los ángulos están mal, deberías haber trabajado con los complementarios para usar coseno en x y seno en y.
Así como los dejaste deberías intercambiar las funciones seno y coseno, es decir, utilizar seno en x y coseno en y.
Hola,
Está bien resuelto, pero yo lo entiendo mejor de la siguiente forma:
Cx = 280 x cos 300º = 140
Cy = 280 x sen 300º = -242,48
El ángulo 300º es el resultado de sumar: 90+90+90+30, es decir, el ángulo desde el eje x dando la vuelta hasta el vector C (representado se ve mejor)
Un saludo
P.D.: me está ayudando muchísimo el contenido de ejercicios resueltos, muchas gracias @Ney!!
Hola! Muchas gracias, tu publicación me ayudó a entender este método de suma de vectores. Pero creo que hay un error, en el problema (el tercer vector) especifica: 30° al este del norte, y en tu diagrama lo que se ve es: 30° al norte del este, no sé si me explico bien, el ángulo θ debería ser 60° básicamente. Creo que de ese modo coincidiría con el resultado del libro 😋
yo lo intente así y no da ninguna de las 2 ahora ;(
noo eso esta bien
yo tambien tenia el libro de fisica universitaria y me daba -2.30 el angulo y no coincidia con los 74 grados del libro de sears y por eso estoy en este lugar aqui y ahora quede como un tonto igual el libro esta bueno