Problema:
Con los vectores de la figura 1.34 use un dibujo a escala para obtener la magnitud y la dirección de a) la resultante
y b) la diferencia
. Con base en sus respuestas, determine la magnitud y la dirección de c)
y d)
.
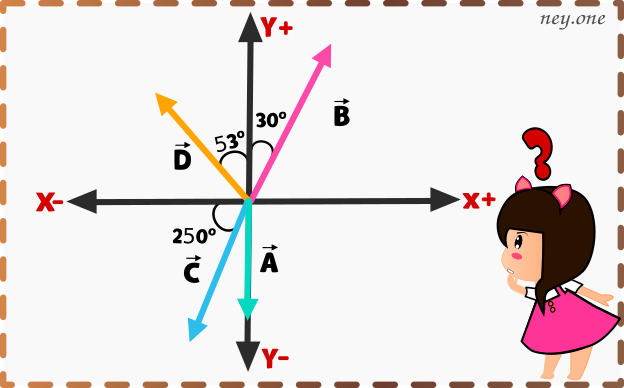
Datos:
Fórmulas:
Donde:
Solución:
a)
Para resolver este problema vamos a encontrar el ángulo del vector . Debido a que el ángulo de un vector siempre parte desde el eje x+.
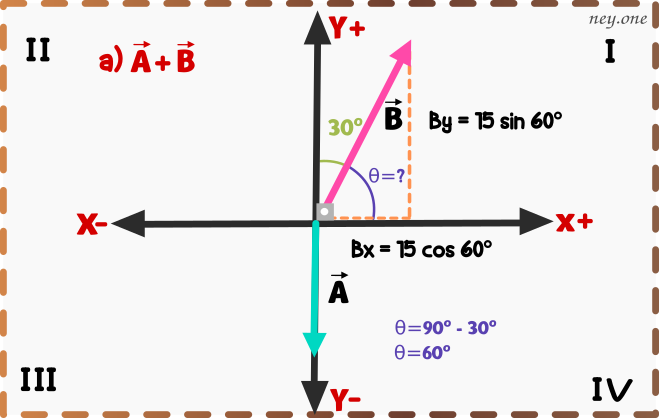
90º es el ángulo total que hay en cada cuadrante y sabemos que entre el vector y el eje y+ del cuadrante I hay 30º, entonces el ángulo del vector
es la diferencia entre 90º y 30º.
Como ya tenemos el ángulo ya podemos encontrar los vectores componentes del vector .
Como el vector se encuentra el el eje y– el valor del vector es negativo.
A continuación usamos la fórmula de Pitágoras para hallar la resultante.
Un vector puede tener un valor positivo o negativo debido al sentido o dirección que tenga; pero la magnitud no tiene sentido entonces la magnitud del vector resultante es:
Bueno, ahora tenemos que hallar el ángulo del vector .
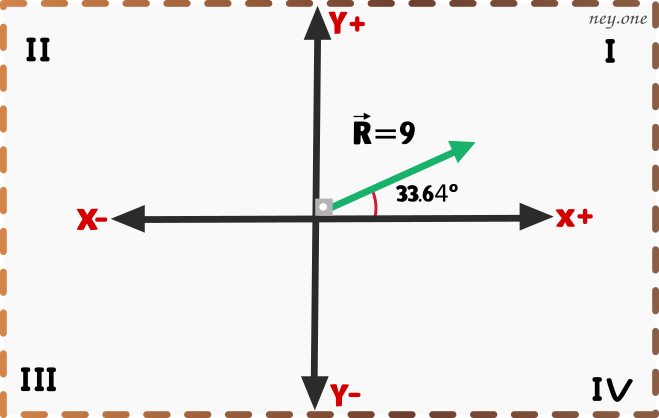
b)
Primero graficamos en el plano cartesiano los vectores y
.
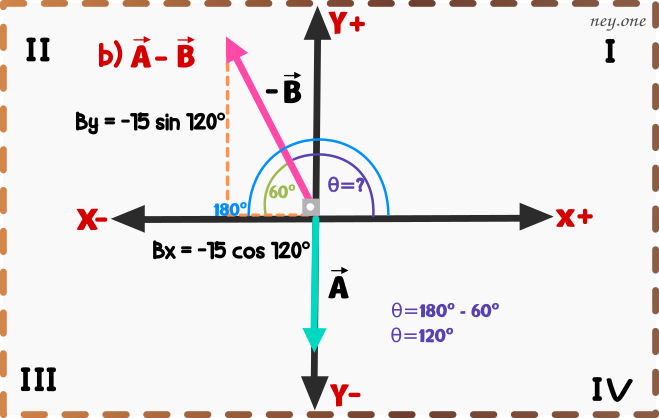
Ahora tenemos que encontrar el ángulo del vector , para ello restamos el ángulo de 180º (que hay entre el eje x positivo y el eje x negativo) con el ángulo de 60º.
Continuando con el problema, toca encontrar los vectores componentes y
.
El valor del vector es negativo por que se encuentra en el eje y negativo.
Con los componentes y
hallamos el vector
Entonces la magnitud del vector es
, otra forma de expresarlo es la siguiente.
Ángulo del vector
Como el decimal 3 no es mayor a 5 lo redondeamos a 70º.
Muy bien, no tenemos que asustarnos con el ángulo . Para entender el resultado del ángulo lo graficamos.
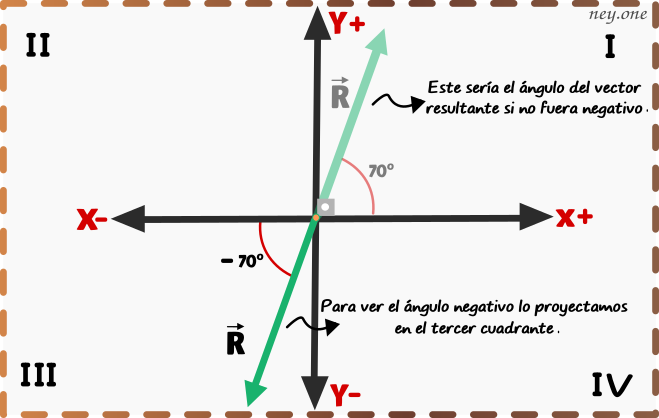
Recordemos que el ángulo de un vector parte siempre del eje x+ y que cada cuadrante tiene un ángulo de 90º, entonces el ángulo del vector es el siguiente.
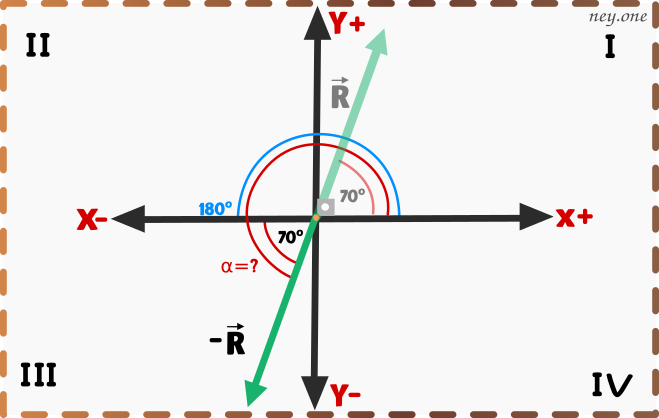
Aclaración:
En este paso nonos interesa si el ángulo es negativo o positivo. Lo que importa es que, del eje x- al vector hay 70º que sumado a el ángulo de 180º da como resultado el ángulo de la resultante.
Entonces el ángulo correcto del vector es:
c)
Graficamos los vectores ,
y
.
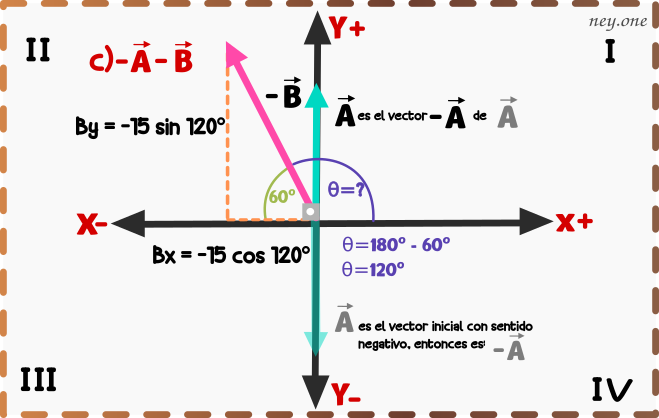
Aclaración:
El vector es negativo porqué su direción apunta al eje y-; pero el vector opuesto de
es
y tiene sentido positivo porque apunta hacia el eje y+.
Bueno, empezamos hallando los vectores componentes y
.
Ya podemos encontrar el vector
La magnitud del vector resultante es:
Finalmente tenemos que encontrar el ángulo del vector
Graficamos el vector con el ángulo negativo para hallar el ángulo más apropiado (esto no indica que el ángulo obtenido de forma analítica este mal).
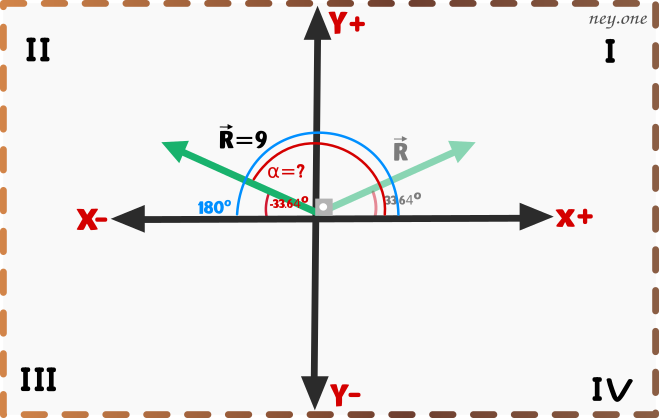
d)
Graficamos
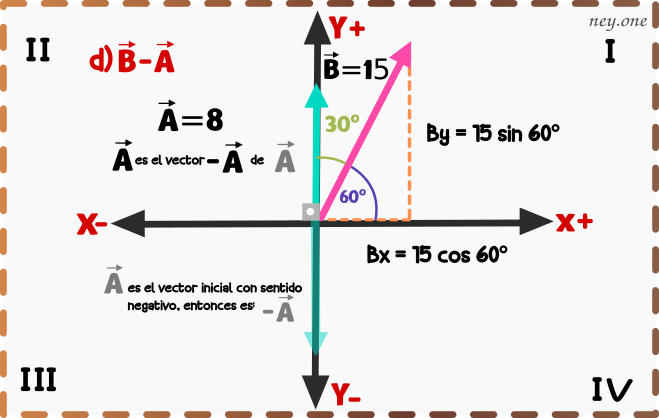
Hallamos los vectores componentes y
El valor del vector es positivo por que la dirección que tiene va hacia el eje y+.
Ahora obtenemos el vector
Entonces la magnitud del vector es
Falta encontrar el ángulo del vector
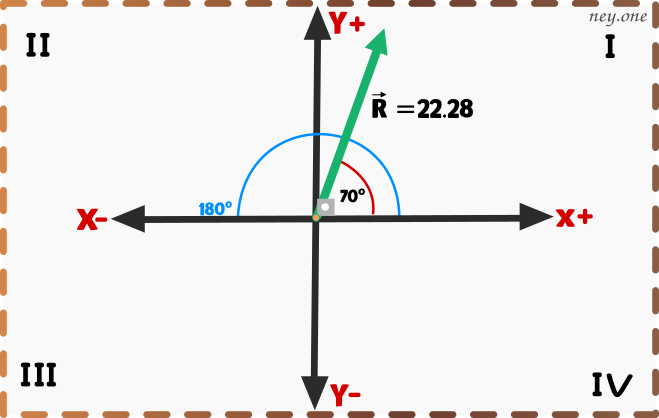
Como el decimal 3 no es mayor a 5 lo redondeamos a 70º.
Bueno, creo que ya puedo ir a peinarme luego de terminar este ejercicio, si me equivoco por favor corríjanme en los comentarios🤣️.



Gracias.
buenas tardes, disculpa una pequeñaduda pero porque by es negativo? si en el grafico esta en el cuadrante 2 de -x y +y, no seria como es la inversa de b en el cuadrante 3 donde -x y -y existen? eso no terminaria cambiando el valor del angulo?
Bro? El último que pedo? Hiciste lo que te convino