Problema :
Dados los vectores y
. Hallar el módulo de
;
,
.
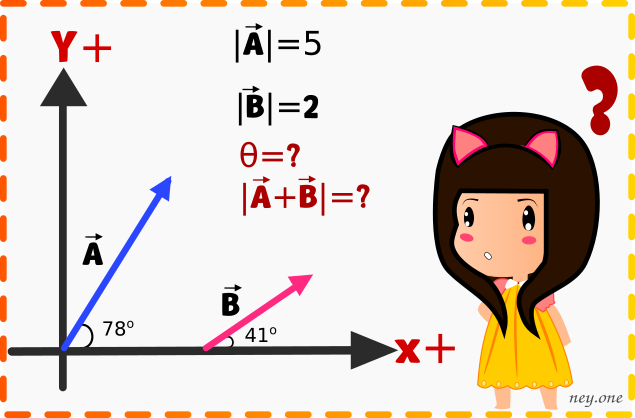
Datos:
Donde:
Vector resultante.
Zeta.
Fórmula:
Solución:
Primero vamos a encontrar el ángulo entre el vector y
, esto lo conseguimos restando el ángulo de 78º grados con el ángulo de 41º grados.
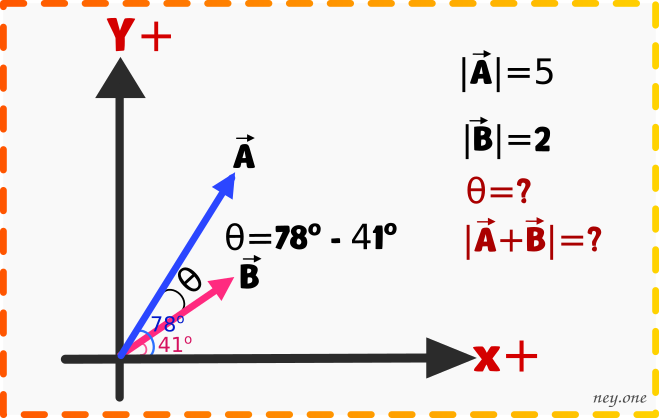
Ahora reemplazamos los datos de los vectores y el ángulo encontrado en la fórmula del coseno.
Redondeando a 2 decimales
Módulo del vector resultante
Conclusión:
El módulo del vector resultante es que es igual a
(también redondeado a 2 decimales).


