Física I – Ejercicio de vectores 01 (Jorge Mendoza Dueñas) | Ney

Publicidad

Problema:

En el sistema mostrado hallar el módulo del vector resultante.

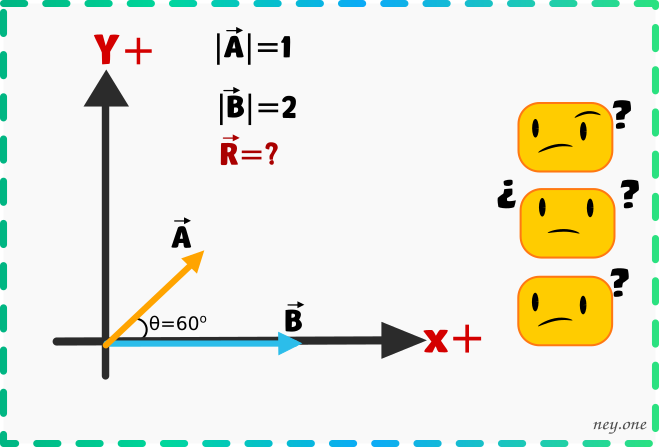
Datos:

$\left\vert \overrightarrow{A}\right\vert = 1$

$\left\vert \overrightarrow{B}\right\vert = 2$

$\theta = 60^o$

Donde:

$\left\vert \overrightarrow{R}\right\vert=$ Vector resultante.

Fórmula:

$\overrightarrow{R} = \sqrt{\overrightarrow{A}^2 + \overrightarrow{B}^2 + 2 \times \overrightarrow{A} \times \overrightarrow{B} \times \cos\theta }$

Publicidad

Solución:

Hallamos el módulo del vector resultante reemplasando los valores del vector $\left\vert \overrightarrow{A}\right\vert$ y $\left\vert \overrightarrow{B}\right\vert$ en el teorema del cosenos.

$\overrightarrow{R} = \sqrt{\overrightarrow{A}^2 + \overrightarrow{B}^2 + 2 \times \overrightarrow{A} \times \overrightarrow{B} \times \cos\theta }$

$\overrightarrow{R} = \sqrt{1^2 + 2^2 + 2 \times 1 \times 2 \times \cos 60^o }$

$\overrightarrow{R} = \sqrt{1 + 4 + 2 \times 1 \times 2 \times \cos 60^o }$

$\overrightarrow{R} = \sqrt{5 + 4 \times \cos 60^o }$

$\overrightarrow{R} = 2.645751311$

Redondeando a 2 decimales

$\overrightarrow{R} = 2.65$

Conclusión:

El módulo del vector resultante es 2.65 y es igual a la $\sqrt{7}$ .

Publicidad

Relacionado

Categorías: FísicaVectores

Tags: ejercicios de vectores resueltoshallar el módulo de un vectorSuma de vectores ley de coseno

Subscribe

0 Comments

Inline Feedbacks

View all comments