
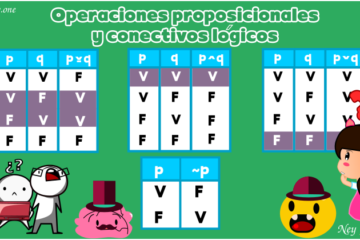
Definición de las leyes de equivalencia lógica
Una Ley de equivalencia lógica es cuando podemos reemplazar una expresión con otra si ambas generan un mismo resultado en la tabla de verdad y este resultado necesariamente tiene que ser una tautología.
Nota: Tautología es cuando el resultado de una proposición es verdadera independiente de los valores de verdad de las proposiciones que lo conforman.
Por ultimo el símbolo o la forma de representar “equivalencia es con el operador lógico de doble implicación o bicondicional”.
Notación de equivalencia: ,
,
A continuación veremos algunas leyes de equivalencia lógica.
Nota: La cantidad de leyes de equivalencia lógica varia dependiendo del libro o lugar donde se busque la información, en un segundo post ampliare estas leyes usando otro libro de referencia.
Leyes de equivalencia lógica
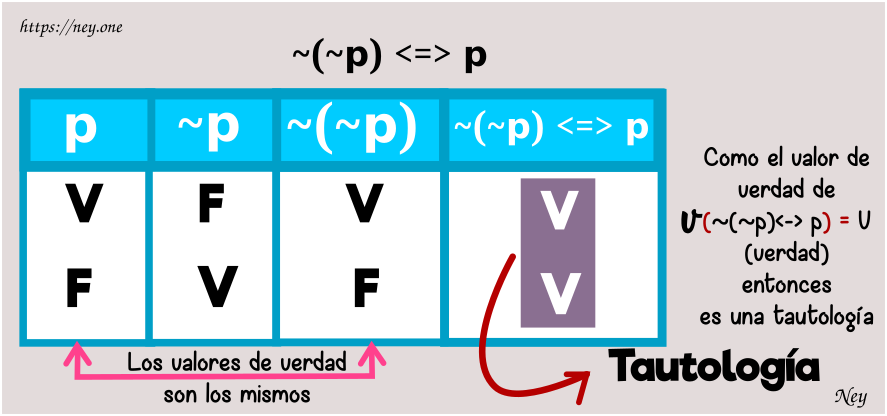
Involución
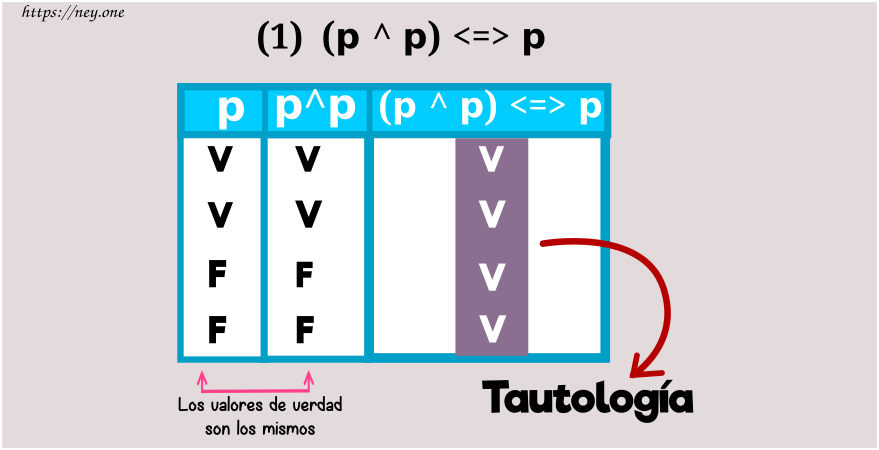
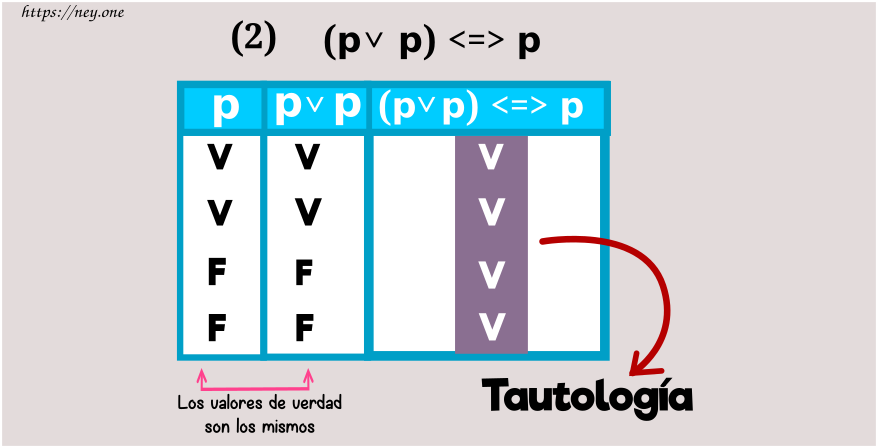
Idempotencia
a) Idempotencia de la conjunción
b) Idempotencia de la disyunción
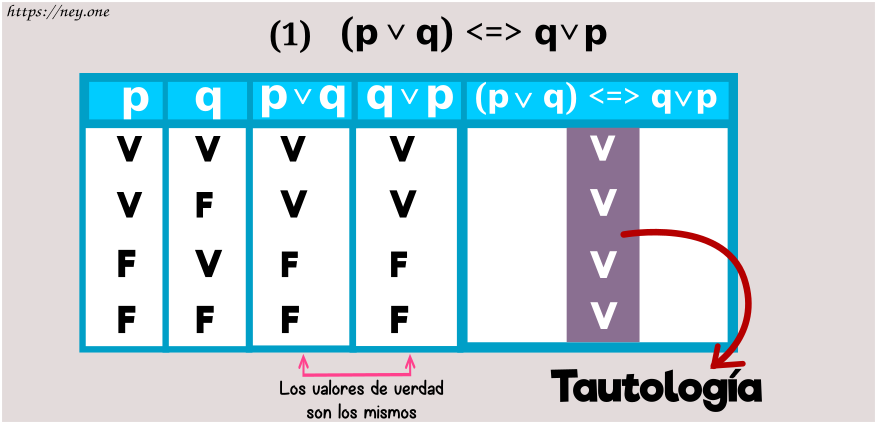
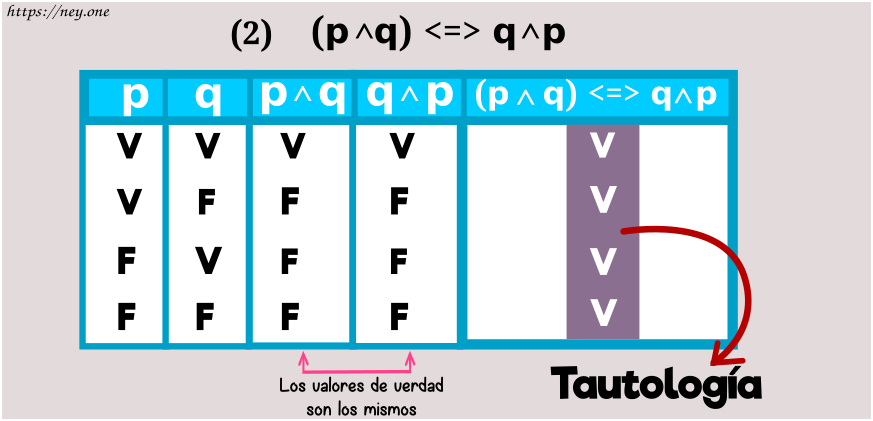
Conmutatividad
a) Conmutatividad de la disyunción
b) Conmutatividad de la conjunción
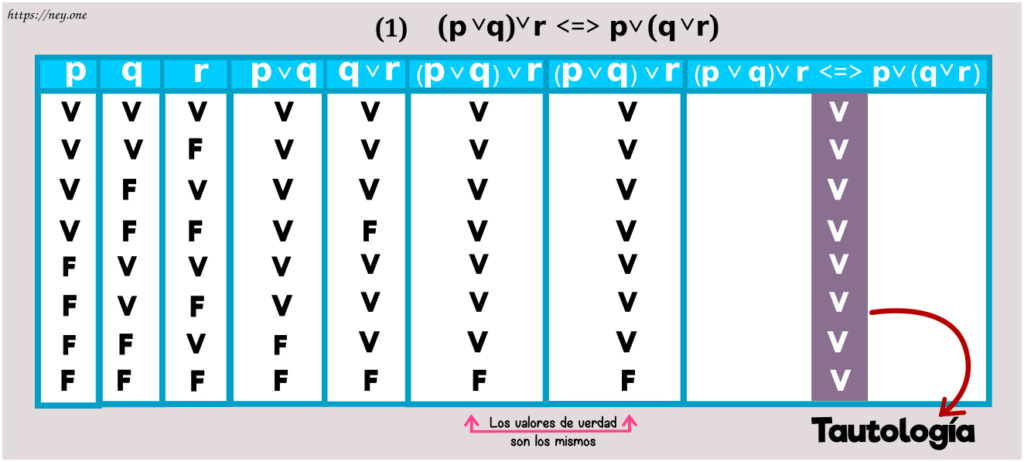
Asociatividad
a) Asociatividad de la disyunción
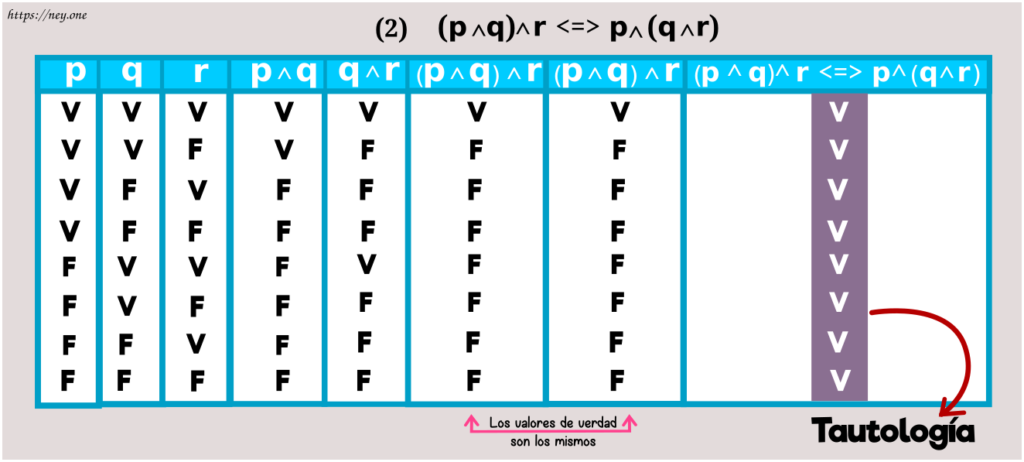
b) Asociatividad de la conjunción
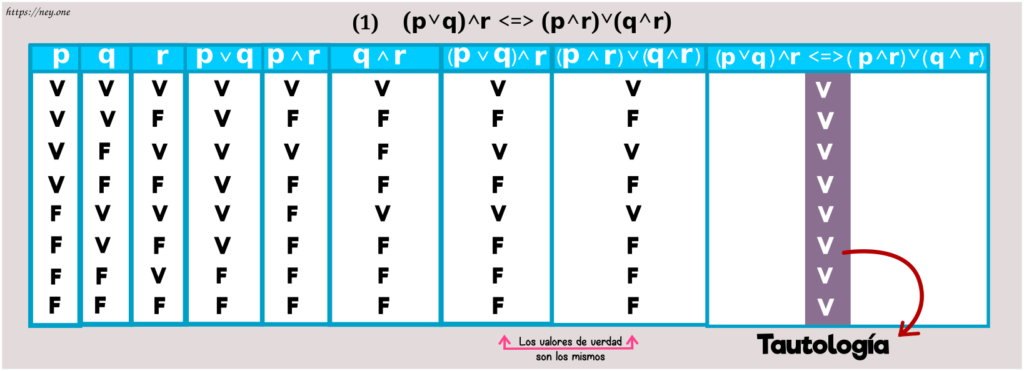
Distributiviadad
a) Distributiviadad de la conjunción respeto de la disyunción
b) Distributiviadad de la disyunción respecto de la conjunción
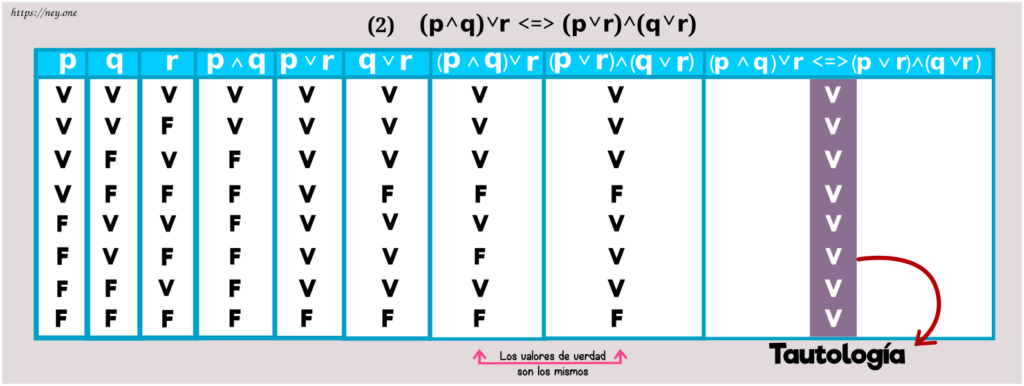
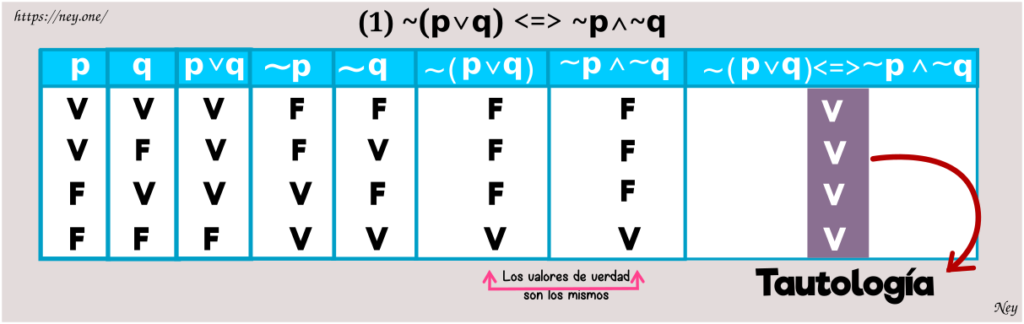
Leyes de De Morgan
a) La negación de una disyunción es equivalente a la conjunción de las negaciones
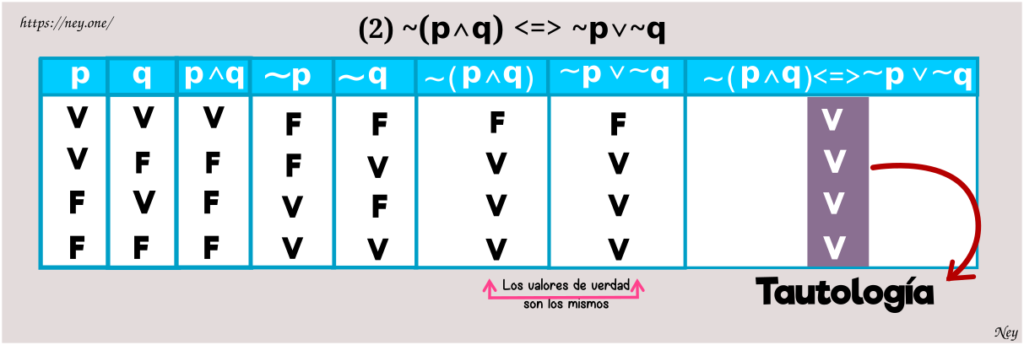
b) La negación de una conjunción es equivalente a la disyunción de las negaciones
Recuerden que yo también soy estudiante 😅️️ y puedo equivocarme así que, si ven un error 🤯️ por favor díganlo en los comentarios, de esta forma todos podemos aprender.😋️

Gracias, me has salvado el díaa <3