Física II - Mecánica de fluidos|Dinámica de fluidos 01

Problema:

Se requiere levantar una moneda de masa m=2.24×10⁻³kg y área A=2.5×10⁻⁴m², soplando sobre ella. Con que velocidad v1 se debe soplar el aire para levantar la moneda?

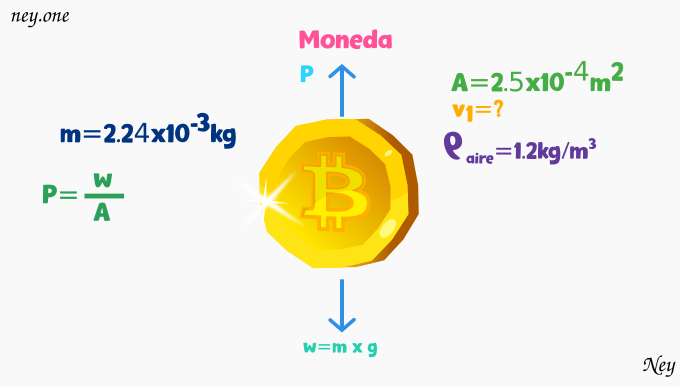
Datos:

$m =2.24 \times 10^{-3}kg$

$A = 2.5 \times 10^{-4}m^2$

$\varrho_{aire}= 1.2kg/m^3$

$g=9.8m/s^2$

$v = ?$

Fórmulas:

(1) $w = m \times g$

(2) $p=\frac{w}{A}$ o $p=\frac{F}{A}$

(3) $\boldsymbol{ p_1 + \frac{1}{2}\times \varrho \times v_1^2 + \varrho \times g \times h_1 = p_2 + \frac{1}{2} \times \varrho \times v_2^2 +\varrho \times g \times h_2 }$

Solución:

Primero:

Tenemos que encontrar el peso (w) o la fuerza que empuja hacia abajo

$w = m \times g$

Reemplazamos los valores de masa y gravedad

$\boldsymbol{w = 2.24 \times 10^{-3}kg \times 9.8m/s^2}$

$w = 0.021952N$

Segundo:

Con el peso (w) de la moneda ya encontrado, ahora podemos encontrar la presión

$\boldsymbol{p= \frac{w}{A}}$

$\Large{\boldsymbol{p= \frac{0.021952N}{2.5 \times 10^{-4}m^2}}}$

$p= 87.808Pa$

Tercero:

A partir de la fórmula (3) encontraremos la v1(velocidad inicial)

$\boldsymbol{ p_1 + \frac{1}{2}\times \varrho \times v_1^2 + \varrho \times g \times h_1 = p_2 + \frac{1}{2} \times \varrho \times v_2^2 +\varrho \times g \times h_2 }$

De esta fórmula podemos notar que no tenemos «h» (altura), ademas suponiendo que la $v_2=0$

entonces tachamos $h_1, h_2, v_2$

$\boldsymbol{ p_1 + \frac{1}{2}\times \varrho \times v_1^2 + \varrho \times g \times \not{h_1} = p_2 + \frac{1}{2} \times \varrho \times \not{v_2^2} +\varrho \times g \times \not{h_2} }$