Física II – Ejercicio de Movimiento armónico simple 012

Problema:

Usted observa un objeto que se mueve en M.A.S. Cuando dicho objeto esta desplazado a 0.600m a la derecha de su posición de equilibrio, tiene una velocidad de 2.20m/s a la derecha y una aceleración de 4.40m/s² a la izquierda. ¿A qué distancia de este punto se desplazará el objeto, antes de detenerse momentáneamente para iniciar su movimiento a la izquierda?

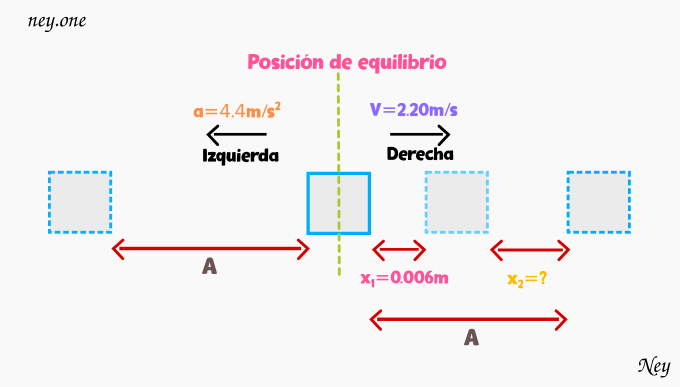
Datos:

$x_{1}= 0.600 m$

$v= 2.20 m/s$

$a= 4.40 m/s^2$

$x_{2}= ?$

Fórmulas:

(1) $a= - w^2 \times x$

(2) $v= w \times \sqrt[2]{A^2 - x^2}$

Donde:

$x_{1}=$ Distancia uno [m].

$v=$ Velocidad [m/s].

$a=$ Aceleración [m/s²].

$x_{2}=$ Distancia dos [m].

Solución:

Si el objeto ya se desplazo 0.600m a la derecha, solo necesitamos saber cual es su amplitud ya que la amplitud es la distancia o desplazamiento máximo a la cual llega la oscilación de un objeto.

Una vez el objeto termina de recorrer la amplitud se detiene un momento y retorna, sabiendo todo esto a la amplitud le restamos la distancia $x_{1}$ y obtenemos la distancia $x_{2}$ que es la distancia que le falta recorrer, en otras palabras $x_{2}$ es el desplazamiento que tendrá el objeto a partir de los 0,600m.

Primero:

Como tenemos distancia y aceleración usamos la fórmula (1) para encontrar la frecuencia.

$a= - w^2 \times x$

x pasa al otro lado a dividir

$\frac{a}{x} = - w^2$

El exponente 2 pasa al otro lado como raíz

${\Large \sqrt[2]{ \frac{a}{x}} = - w}$

Invertimos los lados para mayor compresión

$- w = \sqrt[2]{ \frac{a}{x}}$

Multiplicamos ambos lados por (-1)

${\Large - w \times (-1)= \sqrt[2]{ \frac{a}{x}} \times (-1)}$

$w = - \sqrt[2]{ \frac{a}{x}}$

Reemplazamos

${\Large w = - \sqrt[2]{ \frac{4.40}{0.600}}}$

$w = - 2.708 \frac{rad}{s}$

Segundo:

A partir de la fórmula (2) Despejamos la amplitud

${\Large v= w \times \sqrt[2]{A^2 - x^2}}$

Tomamos la frecuencia angular (w) y la mandamos a dividir al otro miembro o lado

${\Large \boldsymbol{\frac{v}{w}} = \sqrt[2]{A^2 - x^2}}$

La raíz pasa al otro lado con exponente

${\Large \boldsymbol{ ( \frac{v}{w} )^2} = A^2 - x^2}$

x pasa a sumar

${\Large \boldsymbol{ ( \frac{v}{w} )^2} + x^2 = A^2}$

El exponente de A pasa como raíz

${\Large \sqrt[2]{ \boldsymbol{ ( \frac{v}{w} )^2} + x^2} = A}$

Invertimos los lados la ecuación

${\Large A = \sqrt[2]{ \boldsymbol{ ( \frac{v}{w} )^2} + x^2} }$

Reemplazamos los datos

${\Large A = \sqrt[2]{ \boldsymbol{ ( \frac{2.20}{-2.708} )^2} + 0.600^2} }$

${\Large A = \sqrt[2]{ 0.66 + 0.36} }$

${\Large A = 1.0099m }$

Tercero:

Obtenemos el desplazamiento del objeto después de recorrer 0.600m

${\Large x_{2} = A - x_{1}}$

${\Large x_{2} = 1.0099m - 0.600m}$

${\Large x_{2} = 0.4099m }$

Redondeando

${\Large x_{2} = 0.401m }$

Extra:

La fórmula de la amplitud ${\Large A = \sqrt[2]{ \boldsymbol{ ( \frac{v}{w} )^2} + x^2} }$ también la podemos despejarla de la siguiente fórmula ${\Large a_{x}= - A \times w^2 cos (wt + \phi) }$