Física II – Ejercicio de Mecánica de fluidos Flotación 03

Problema:

Una boya cilíndrica de 1000 kg y 0.600 m de diámetro flota verticalmente en agua salada. Calcule la distancia adicional a la cual la boya se hundirá, si un hombre de 70.0 kg se pone de pie sobre ella.

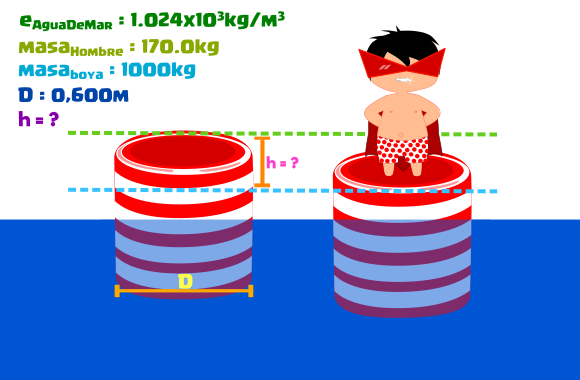
Datos:

$m_{boya} = 1000kg$

$D = 0.600m$

$Di\acute{a}metro = 0.600m$

$h = ?$

$m_{Hombre} = 70.0kg$

$\varrho_{agua} = 1000kg/m^3$

$\varrho_{AguaDeMar} = 1024 \times10^3 kg/m^3$

Formulas:

(1) $V = A \times h$

(2) $A = \Pi \times \frac{D^2}{4}$

(3) $W = m \times g$

(4) $B = \times g$

(5) $\varrho = \frac{m}{V}$

Donde:

$m =$ Masa [kg]

$D =$ Diámetro [m]

$h =$ Altura [m]

$\varrho =$ Densidad [kg/m³]

$V =$ Volumen [m³]

$g =$ Gravedad [m/sg²]

$B =$ Fuerza de empuje [N]

$A =$ Area [m²]

Solución:

Tenemos que hallar la altura a la cual se encuentra la boya inicialmente y luego hallar la altura de la boya con el hombre enésima, finalmente restamos la altura final con la inicial, para saber cuanto se hundió la boya.

Primero:

Hacemos sumatoria de fuerzas en «Y», sin contar el peso del hombre.

$\Sigma F y = 0$

$B - W_{boya} = 0$

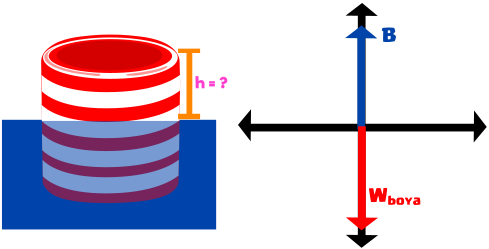
Reemplazamos las formulas (3) y (4) en la fuerza de empuje y del peso.

$m_{AguaDeMar} \times g - m_{boya} \times g = 0$

Ahora, de la formula (5) despejamos la masa.

$\varrho = \frac{m}{V}$

$m = \varrho \times V$

Y la reemplazamos en la fuerza de empuje.

$\varrho_{AguaDeMar} \times V_{AguaDeMar} \times g - m_{boya} \times g = 0$

Multiplicamos toda la ecuación por (1/g) para eliminar la gravedad.

$\varrho_{AguaDeMar} \times V_{AguaDeMar} - m_{boya} = 0$

Usamos la formula (1) reemplazamos en el volumen del agua de mar.

$\varrho_{AguaDeMar} \times A_{boya} \times h - m_{boya} = 0$

Despejamos la altura.

$h = \frac{m_{boya}}{\varrho_{AguaDeMar} \times A_{boya}}$

Antes de reemplazar los valores en formula de la altura, debemos hallar el área de la boya.

$A = \Pi \times \frac{D^2}{4}$

$A = \Pi \times \frac{(0.600m)^2}{4} = 0.28274m^2$

Reemplazamos los valores numéricos en la formula altura.

$h = \frac{1000kg}{1.024\times 10^3 \frac{kg}{m^3} \times 0.28274m^2}$

$h = 3.454412805m$

Segundo:

Ahora para conocer cuanto se a hundido la boya con el peso del hombre, volvemos hacer sumatoria de fuerzas en el eje «Y» con el peso del hombre.

$\Sigma F y = 0$

$B - W_{Hombre} - W_{boya} = 0$

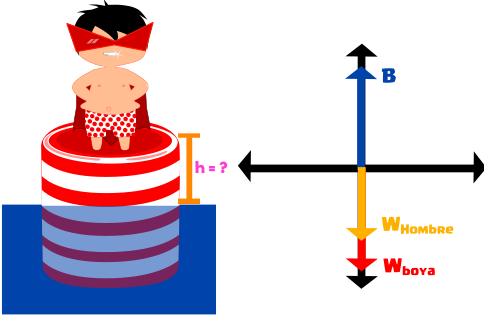
Reemplazamos las formulas (3) y (4) en la fuerza de empuje, el peso del hombre y el peso de la boya.

$m_{AguaDeMar} \times g - m_{Hombre} \times g - m_{boya} \times g = 0$

Multiplicamos toda la ecuación por (1/g) para eliminar la gravedad.

$m_{AguaDeMar} - m_{Hombre} - m_{boya} = 0$

Usamos la formula (5) despejamos la masa y la reemplazamos en la masa del agua de mar.

$\varrho = \frac{m}{V}$

$m = \varrho \times V$

$\varrho_{AguaDeMar} \times V_{AguaDeMar} - m_{Hombre} - m_{boya} = 0$

Usando la formula (1) y la reemplazamos en el volumen del agua de mar.

$\varrho_{AguaDeMar} \times A_{boya} \times h - m_{Hombre} - m_{boya} = 0$

Ahora usamos la formula (2) y la reemplazamos en el área de la boya.

$\varrho_{AguaDeMar} \times \Pi \times \frac{D^2}{4} \times h - m_{Hombre} - m_{boya} = 0$

Despejamos la altura.

$\varrho_{AguaDeMar} \times \Pi \times \frac{D^2}{4} \times h = m_{Hombre} + m_{boya}$

$h = \frac{m_{Hombre} + m_{boya}}{\varrho_{AguaDeMar} \times \Pi \times \frac{D^2}{4}}$

Reemplazamos los valores numéricos.

$h = \frac{70.0kg + 1000kg}{1.024 \times 10^3 \frac{kg}{m^3} \times \Pi \times \frac{(0.600m)^2}{4}}$

$h = 3.695655145m$

Tercero:

La distancia adicional a la que se hundió la boya es la diferencia entre la altura final y la altura inicial.

$h_{hundida} = h_{final} - h_{inicial}$

$h_{hundida} = 3.695655145m - 3.454412805m$

$h_{hundida} = 0.2412m$

Conclusión:

Cuando un hombre de 70.0kg, sube a la boya esta se hunde 0.2412 m.

Si encuentras algún error o algún otro detalle que se me hubiera escapado🤯 por favor dejalo en los comentarios, para que pueda corregirlo.

Física II – Ejercicio de Mecánica de fluidos Flotación 03

Publicado por Ney en 13 noviembre, 201913 noviembre, 2019

Relacionado

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015

Física II – Ejercicio de Mecánica de fluidos Flotación 03

Publicado por Ney en 13 noviembre, 201913 noviembre, 2019

Relacionado

Entradas relacionadas

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015