Física I – Suma o adición de vectores método analítico

Introducción:

Hola chicos, en este nuevo tema debo comentarles que… me costo recordar el teorema de senos y la verdad me llevo a preguntarme ¿Cómo termine el colegio?.

Yo recordaba que la fórmula de senos funcionaba de otra manera y como los ejercicios que hice previo al tema no me salían bien 😅️ me llevo a desempolvar un libro de física y a buscar información en internet. Ya que no puedo escribir un tema de algo que no estoy entendiendo bien y bueno mejor empecemos con el tema.

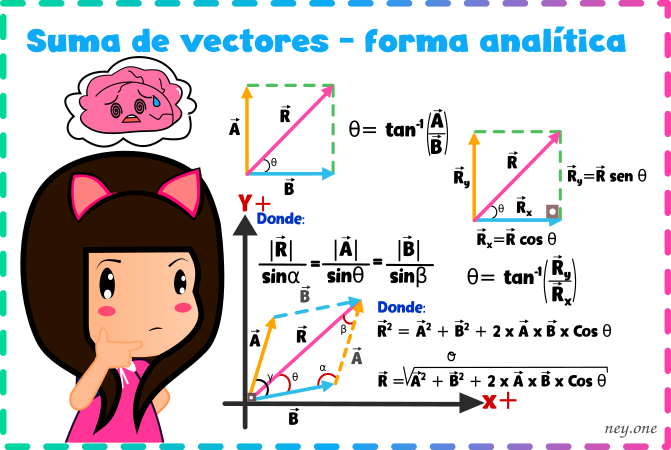
1. Suma de vectores colineales

Vamos a encontrar o determinar el vector resultante de los vectores colineales sumando los módulos de los vectores teniendo en cuenta el sentido que estos tengan según el eje de coordenadas.

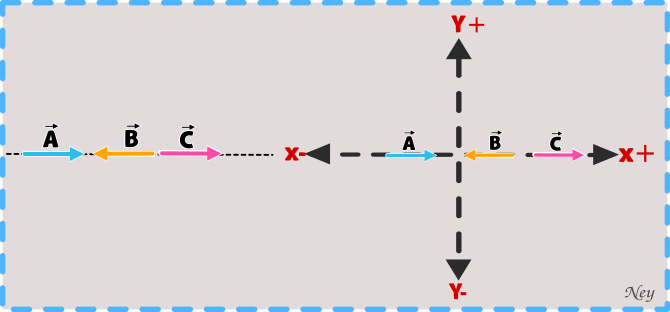
Ejemplo1.

Encontrar el vector resultante de los siguientes vectores colineales sabiendo que el módulo o norma de los vectores son los siguientes:

$\left\vert \overrightarrow{A}\right\vert = 5$ , $\left\vert \overrightarrow{B}\right\vert = 3$ , $\left\vert \overrightarrow{C}\right\vert = 4$ , $\left\vert \overrightarrow{D}\right\vert = 1$

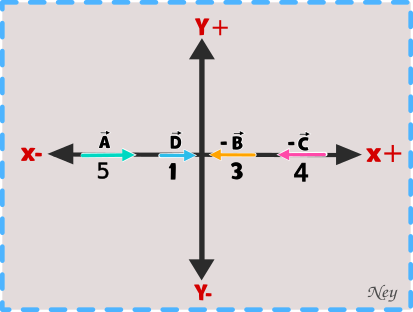
Solución:

Parte de la solución consiste en identificar correctamente el sentido de cada vector.

El sentido del vector $\overrightarrow{A}$ es positivo; porque va hacia el eje x positivo.
El sentido del vector $\overrightarrow{B}$ es negativo; porque va hacia el eje x negativo.
El sentido del vector $\overrightarrow{C}$ es negativo; porque va hacia el eje x negativo.
El sentido del vector $\overrightarrow{D}$ es positivo; porque va hacia el eje x positivo.

Entonces el vector resultante es:

$\overrightarrow{R} = \overrightarrow{A} + \overrightarrow{B} + \overrightarrow{C} + \overrightarrow{D}$

$\overrightarrow{R} = 5 + (-3) + (-4) + 1$

$\overrightarrow{R} = 5 - 3 -4 + 1$

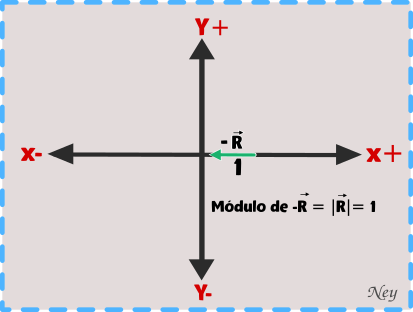
$\overrightarrow{R} = -1$ y el módulo es $\left\vert \overrightarrow{R}\right\vert = 1$

2. Componentes de un vector

Se denominan componentes de un vector a todos los vectores que sumados o restados dan como resultado un nuevo vector, esto lo podemos ver en el método del triangulo y el método del polígono.

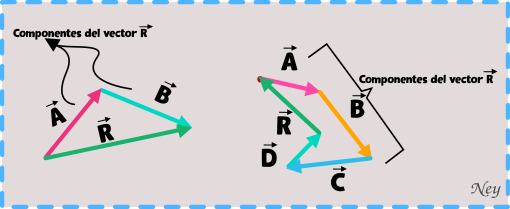
3. Componentes rectangulares de un vector original en 2 dimensiones

Los vectores componentes forman entre si un ángulo de 90º y también podemos decir que son proyecciones de un vector x (un vector cualquiera) en el eje horizontal y vertical.

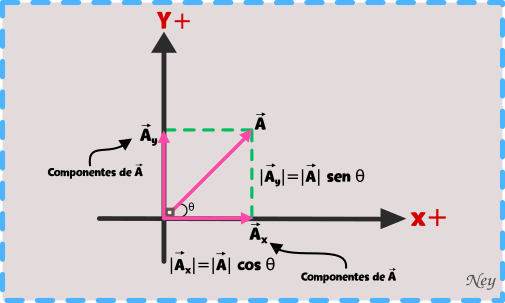
Para hallar el vector resultante de los componentes rectangulares usamos el teorema de Pitágoras.

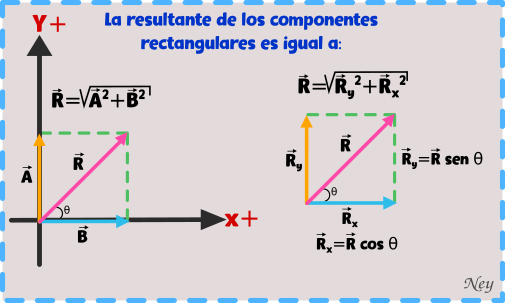
Si queremos encontrar el ángulo de la resultante de los componentes rectangulares usamos la fórmula de la tangente.

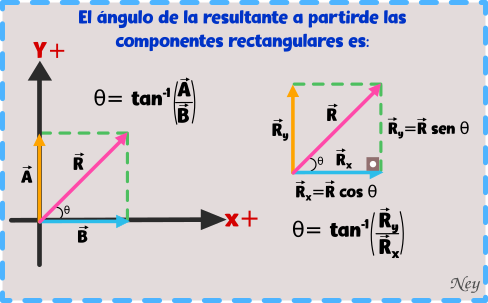
Ejemplo 2.

Encontrar el valor de las componentes y el ángulo α sabiendo que el ángulo de del vector $\overrightarrow{A}$ es 33º.

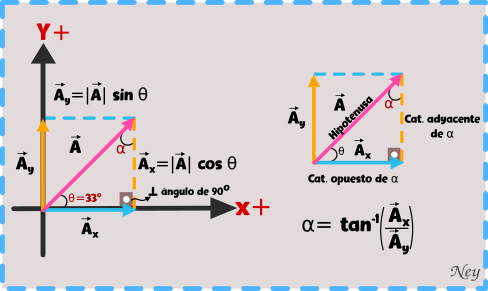
Solución:

$\overrightarrow{A _x} = \overrightarrow{A} \cos 33^o =4.19335u$

$\overrightarrow{A _y} = \overrightarrow{A} \sin 33^o =2.72319u$

Como la suma de los ángulos en un triángulo rectángulo debe ser igual a 180º y tenemos 2 de los ángulos, entonces encontramos el ángulo α de la siguiente forma.

$\Large{ \tan \boldsymbol{\alpha} = \frac{\overrightarrow{A _x}}{\overrightarrow{A _y}} }$

$\Large{ \tan \boldsymbol{\alpha} = \frac{4.19335u}{2.72319u} }$

$\tan \boldsymbol{\alpha} = 1.539866u$

$\boldsymbol{\alpha} = \tan^{-1} (1.539866u)$

$\alpha = 57^o$

Otra forma de hallar el ángulo de α es la siguiente:

$180^o = \theta + \perp + \alpha$

$180^o = 33^o + 90^o + \alpha$

$180^o = 123^o +\alpha$

$\alpha =180^o - 123^o$

$\alpha = 57^o$

comprobando que la suma de todos los ángulos da 180º

$180^o = \alpha + \perp + \theta$

$180^o = 33^o + 90^o + 57^o$

$180^o = 180^o$

4. Suma de 2 vectores en 2 dimensiones forma analítica

La suma de 2 vectores da como resultado el vector resultante, este vector es hallado mediante el teorema de cosenos.

Teorema o ley de coseno

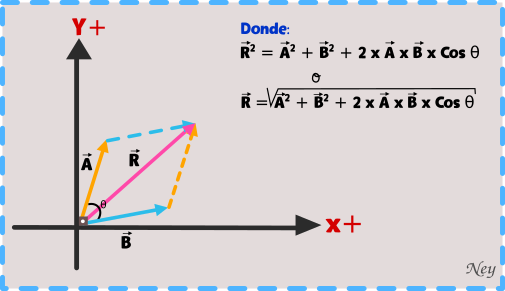
Para la resta o sustracción de 2 vectores de forma analítica usamos la anterior formula modificada de la siguiente manera:

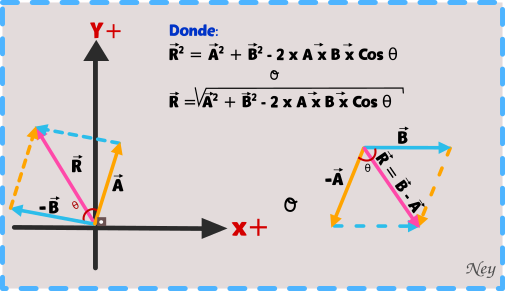
Teorema de cosenos si el ángulo es 90º

Si $\theta = 90^o \text{ entonces} \cos 90^o = 0$

$\overrightarrow{R} = \sqrt{\overrightarrow{A}^2 + \overrightarrow{B}^2 + 2 \times \overrightarrow{A} \times \overrightarrow{B} \times \cos 90^o}$

$\overrightarrow{R} = \sqrt{\overrightarrow{A}^2 + \overrightarrow{B}^2 + 2 \times \overrightarrow{A} \times \overrightarrow{B} \times 0}$

$\overrightarrow{R} = \sqrt{\overrightarrow{A}^2 + \overrightarrow{B}^2 }$ … $\text {esto viene siendo el teorema de}$ $pit\acute{a}goras$

Finalmente la dirección o el ángulo de un vector resultante se halla con el teorema o la ley de senos.

Teorema o ley de senos

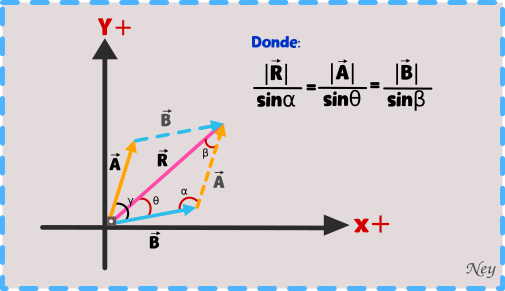
Ejemplo 3.

En el siguiente sistema encontrar el módulo del vector resultante.

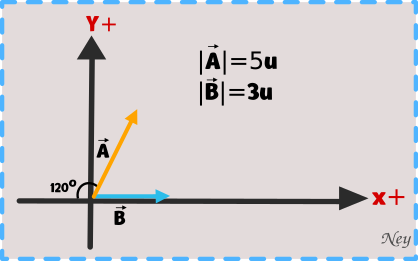
Solución:

Hallamos el módulo del vector resultante con la formula de cosenos.

$\overrightarrow{R} = \sqrt{\overrightarrow{A}^2 + \overrightarrow{B}^2 + 2 \times \overrightarrow{A} \times \overrightarrow{B} \times \cos\theta }$

$\overrightarrow{R} = \sqrt{\overrightarrow{A}^2 + \overrightarrow{B}^2 + 2 \times \overrightarrow{A} \times \overrightarrow{B} \times \cos\gamma }$

$\overrightarrow{R} = \sqrt{\overrightarrow{5}^2 + \overrightarrow{3}^2 + 2 \times \overrightarrow{5} \times \overrightarrow{3} \times \cos 60^o }$

$\overrightarrow{R} = 7u$

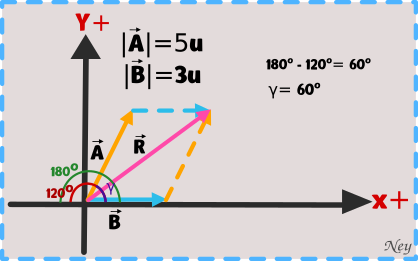
Ejemplo 4.

Dos vectores de 10 y 8 unidades de longitud, forman entre sí un ángulo de 90º. Encontrar la magnitud de la diferencia de estos vectores y el ángulo con respecto al vector con mayor longitud.

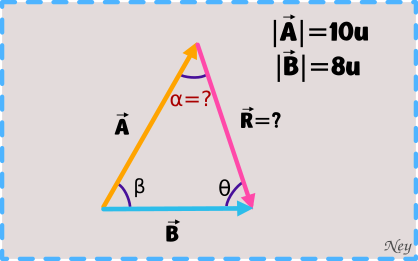
Solución:

El vector mayor es el que tiene un módulo más grande.

La diferencia o resta entre estos 2 vectores da como resultado un vector resultante y para hallar su magnitud o módulo usamos el teorema del coseno.

$\overrightarrow{R} = \sqrt{\overrightarrow{A}^2 - \overrightarrow{B}^2 + 2 \times \overrightarrow{A} \times \overrightarrow{B} \times \cos \theta}$

$\overrightarrow{R} = \sqrt{\overrightarrow{A}^2 - \overrightarrow{B}^2 + 2 \times \overrightarrow{A} \times \overrightarrow{B} \times \cos \beta}$

$\overrightarrow{R} = \sqrt{10^2 + 8^2 + 2 \times 10 \times 8 \times \cos 90^o}$

Como cos 90º es igual a cero, todo y todo lo que es multiplicado por cero da cero la formula queda así

$\overrightarrow{R} = \sqrt{10^2 + 8^2}$

$\overrightarrow{R} = 12.806u$

Ahora encontramos el ángulo con respecto al vector con mayor longitud.

$\Large{ \frac{ \overrightarrow{R}}{\boldsymbol{\sin \beta}} = \frac{ \overrightarrow{A}}{\sin \theta} = \frac{\overrightarrow{B}}{\sin \alpha}}$

$\Large{ \frac{ \overrightarrow{R}}{\boldsymbol{\sin \beta}} = \frac{ \overrightarrow{B}}{\sin \alpha}}$

Despejamos alfa $(\alpha)$

$\Large{ \overrightarrow{R} = \frac{ \overrightarrow{B}}{\boldsymbol{\sin \alpha}} \times \sin \beta}$

$\Large{ \overrightarrow{R} \times \sin \alpha = \overrightarrow{B} \times \sin \beta}$

$\Large{\sin \alpha = \frac{\overrightarrow{B} \times \boldsymbol{\sin \beta}} {\overrightarrow{R}}}$

$\Large{\alpha = \sin^{-1}\Bigg( \frac{\overrightarrow{B} \times \boldsymbol{\sin \beta}} {\overrightarrow{R}}\Bigg)}$

Reemplazamos los valores de los vectores y el ángulo

$\Large{\alpha = \sin^{-1}\Bigg( \frac{8u \times \boldsymbol{\sin 90^o}} {12.806u}\Bigg)}$

$\boldsymbol{\alpha} = 38.660^o$ $\text{o}$ $38^o39^o38.51$

Bueno, con estos ejemplos termia la explicación sobre el tema de suma de vectores de forma analítica, espero les sea de ayuda y si encuentran algún error por favor dejarlo en los comentarios.

$\not{3}$

Física I – Suma o adición de vectores método analítico

Publicado por Ney en 8 junio, 20208 junio, 2020

Relacionado

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015

Física I – Suma o adición de vectores método analítico

Publicado por Ney en 8 junio, 20208 junio, 2020

Relacionado

Entradas relacionadas

Física

Concepto de física

Física

Ejercicio de Movimiento armónico simple| Energía 016

Física

Física II – Ejercicio de Movimiento armónico simple| Energía 015