Problema:
Una marinera en un velero pequeño se topa con vientos cambiantes. Navega 2.00 km al este, luego 3.50 km al sureste y después otro tramo en una dirección desconocida. Su posición final es 5.80 km directamente al este del punto inicial. Determine la magnitud y la dirección del tercer tramo. Dibuje el diagrama de suma vectorial y demuestre que concuerda cualitativamente con su solución numérica.
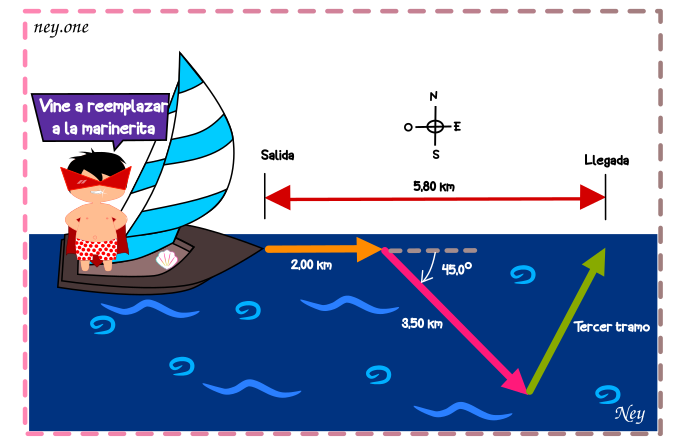
Datos:
Donde:
Fórmulas:
Solución:
Al resolver este problema no necesitaremos usar muchas formulas; pero si graficar bastante, empecemos.
Primero:
Restamos el vector A con la distancia x (que va desde el punto inicial del vector A al punto final del vector C). Al resultado de esta resta llamaremos .
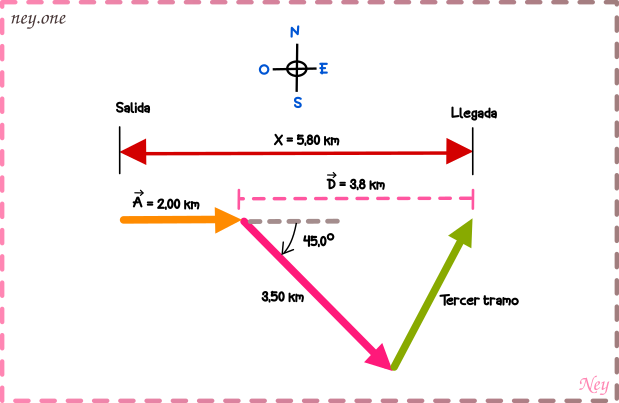
Segundo:
Descomponemos el vector en sus componentes «x» y «y».
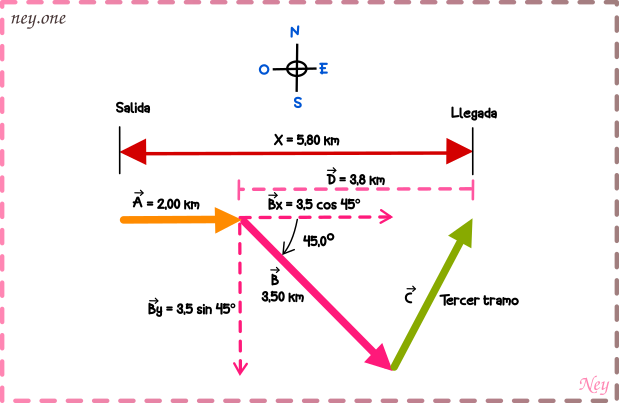
Tercero:
Ahora restamos a
, con esta resta lo que vamos a conseguir es encontrar el componente en x del vector
(que luego utilizaremos para encontrar el propio vector
).
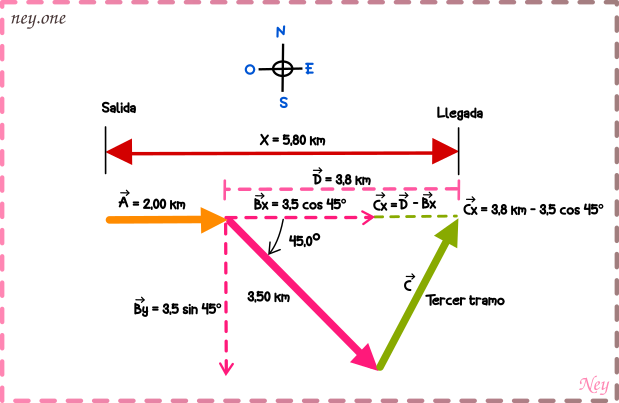
Cuarto:
Ahora desplasamos el componente asta llegar al vector
.
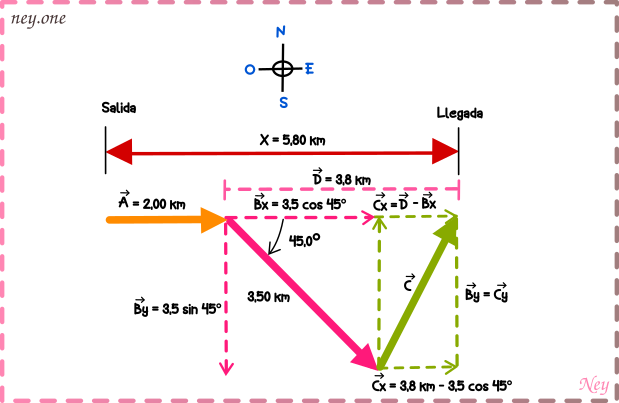
Notemos que el componente es igual componente
Quinto:
Como ya tenemos los componentes «x» y «y» del , toca encontrar el vector
.
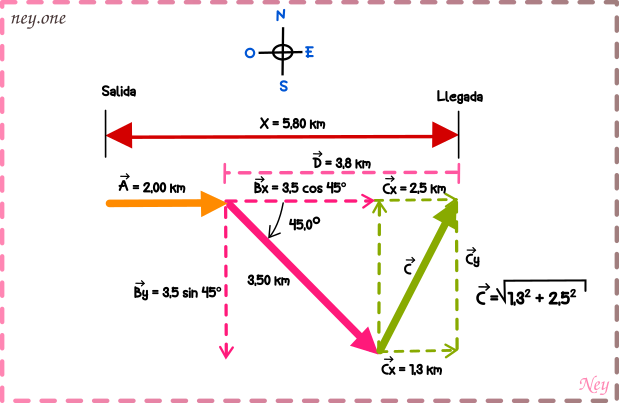
Entonces la magnitud del vector es:
Sexto:
Con los valores de los componentes del vector también podemos encontrar el ángulo.
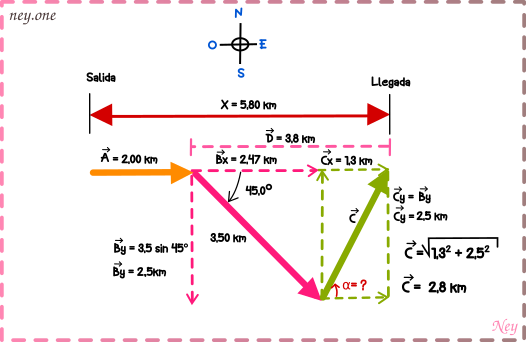
Con esto ya tenemos la magnitud y la dirección del vector o mejor dicho del ultimo tramo del velero.



el arctan de 25/13 da es 62,5 no 27
Oh, me equivoque al copiar el ejercicio de mi cuaderno voy a corregirlo hoy, muchas gracias.
gracias te amo
Gracias:)))
Crees en la posibilidad de competirte algunos ejercicios, con sus respectivas soluciones, para que los publiques?